析取消去規則

析取消去規則(elimination rule of disjunction)是推理規則的一種，如果前提p∨q和¬p均為真，則可得結論命題q為真，由此得到的推理規則稱為析取消去規則。

基本介紹

• 中文名：析取消去規則
• 外文名：rule for ∨-elimination
• 所屬學科：數學（形式邏輯）
• 簡介：某些自然推理系統中的推理規則
• 內容：若前提p∨q和¬p均為真，則q為真

基本介紹

析取消去規則是某些自然推理系統中的推理規則之一。簡記為∨E或V_-。可表述為：

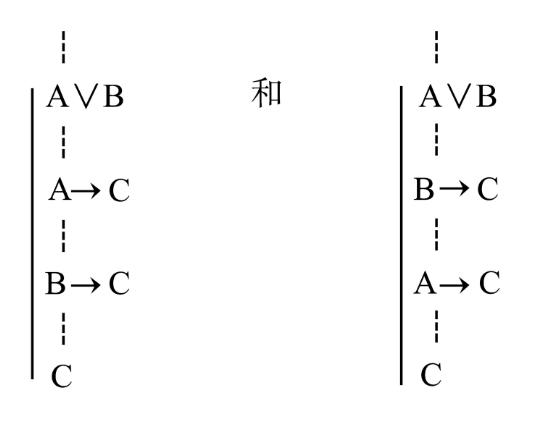
若Γ├A∨B，Δ∪{A}├C並且Λ∪{B}├C，則Γ∪Δ∪Λ├C。

其中Γ、Δ和Λ是任意的公式的集合，A、B、C是公式，├是推出關係。

這一規則意為：若Γ可以推出A∨B，Δ和A可推出C，Λ和B亦可推出C，則Γ、Δ和Λ可以推出C。這一規則又可用如下的圖式來表示：

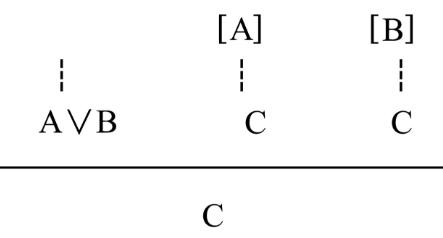圖1

圖式中的公式A、B的外面打了方括弧[]，表示使用了這一規則之後，方括弧內的公式A和B被消去，不再是推理的前提。

也可以表述為如下的圖式：

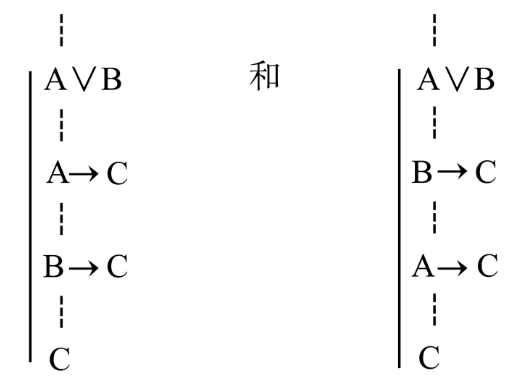圖2

例如在命題演算中，

從p→r，q→r，p∨q，可以推出r;

從p→(q∨p)，q→(q∨p)，q∨p，可以推出q∨p。

在謂詞演算中，

從(∀x)F(x)→(F(x)∨G(x ))，(∀x)G(x)∨(F(x)∨G(G(x ))，(∀x)F(x)∨(∀x)G(x)，可以推出F(x)∨G(x)。

普通邏輯中二難推理的簡單構成式相當於用析取詞消去規則進行的推演。

由析取式的邏輯特徵引出的規則

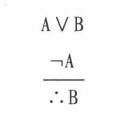
析取式的邏輯特徵是：一個析取式真，若且唯若兩個支命題至少有一個真，因此有析取消去（否定）式和析取引入兩個有效推理式。

析取消去規則（簡記V-）

析取引入規則（簡記V+）

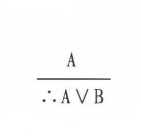
如下是析取消去規則的例示：

“佳士德拍賣公司拍賣的圓明園獸首或者拍賣成功或者流拍。圓明園獸首沒有拍賣成功。所以，圓明園獸首流拍。”

一個析取式是真的，那么其析取支至少有一個真。因此，由A∨B和¬A為真推出B必為真。因為如果B不是真的則A∨B也不可能真，這與A∨B為真的假定是矛盾的。

但是由A∨B和A為真，卻推不出B的真假，因為析取式只要有一個析取支真就是真的。因此，當A∨B和A為真時，B可以是真的也可以是假的，即B的真假無法確定。所以，否定析取式的一個析取支必然推出肯定其另一個析取支的結論，但肯定析取式的一個析取支卻推不出關於另一個析取支的結論。即如下推理式是無效的：

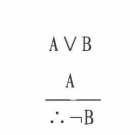
析取引入規則在日常思維中用得很少，但在推理有效性證明中這個推理式有重要作用。