在物理學上,朗道-利夫希茲-吉爾伯特方程(Landau–Lifshitz–Gilbert),是以列夫·達維多維奇·朗道、葉夫根尼·利夫希茨和T·L·吉爾伯特命名的物理方程,以差分方程為基礎闡述一個進動磁性粒子的自發磁化。由T·L·吉爾伯特修改列夫·達維多維奇·朗道、葉夫根尼·利夫希茨的方程得到。該方程可以描述無外場作用下粒子受平均場作用而產生的運動。該方程直接暗示了自旋系統存在孤子。 朗道-利夫希茲方程是非線性偏微分方程,該方程有單一孤子的嚴格解,對於多孤子情形,可以採取數值方法求解。該方程在在不同情形下模擬微磁性磁場的鐵磁性磁場,尤其孤子於磁場的時閾行為。
基本介紹
- 中文名:朗道-利夫希茲方程
- 外文名:Landau–Lifshitz–Gilbert
朗道-利夫希茲方程,物理意義,固體物理學,
朗道-利夫希茲方程
1955年吉爾伯特由一個依賴於磁場的時間導數取代了朗道-利夫希茲的阻尼項:
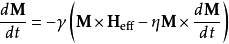

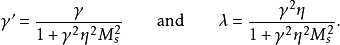
物理意義
平均場引發的自我驅動往往具有自持效果,這種效果的體現就是一群粒子可以形成穩定的孤子波。這就是磁性孤子。
