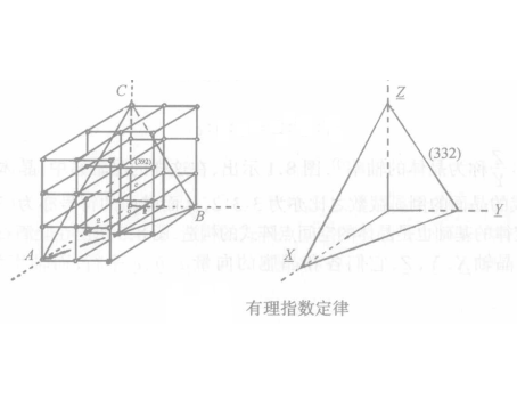
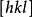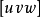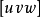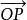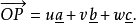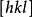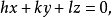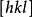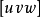基本介紹
- 中文名:有理指數定律
- 外文名:law of rational indices
- 別名:整數定律、阿羽依定律定律
- 屬性:單晶體外形晶面的一條實驗定律
定義,詳細分析,
定義
就每一品種的晶體來說,必可覓得一套稱為晶軸系的坐標軸系,從而使晶體上每個晶面在這三個晶軸上的倒易截數成簡單的互質整數之比,即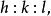 這一規律性稱為有理指數定律,整數
這一規律性稱為有理指數定律,整數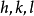 稱為晶面的指數,符號
稱為晶面的指數,符號 稱為晶面的記號,有理指數定律突出地反映了晶體的點陣式構造。
稱為晶面的記號,有理指數定律突出地反映了晶體的點陣式構造。

 圖1(a)有理指數定律
圖1(a)有理指數定律 圖1(b)有理指數定律
圖1(b)有理指數定律詳細分析
設晶體的晶胞系由向量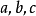 所規定,現以點陣點O為原點,向量
所規定,現以點陣點O為原點,向量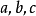 為三個坐標軸,而某一平麵點陣的平面在三個坐標軸上的截點為
為三個坐標軸,而某一平麵點陣的平面在三個坐標軸上的截點為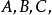 如圖1中所示在圖中,這個平面的截長為
如圖1中所示在圖中,這個平面的截長為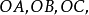 截數為
截數為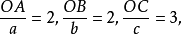 而倒易截數為
而倒易截數為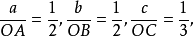 設在上述平麵點陣中有一點陣點為P,並設
設在上述平麵點陣中有一點陣點為P,並設
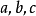
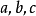
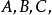
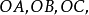
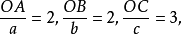
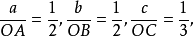
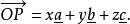
在此,P點的坐標 必為有理數,且應滿足平面的方程:
必為有理數,且應滿足平面的方程:




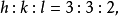

 圖2
圖2綜上所述,我們就可以這樣來選取晶軸系 設取
設取 各與晶胞的
各與晶胞的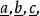 平行,並使
平行,並使


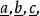
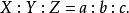

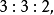


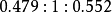
 圖3(a)
圖3(a) 圖3(b)
圖3(b)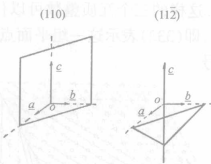 圖3(c)
圖3(c)晶體上每個晶面一般為原子或原子團按晶體點陣中間距較大的平麵點陣鋪成的平面,而這樣的平麵點陣一般具有較為簡單的指數,圖4示出點陣中各平麵點陣組的間距隨其指數的增大而遞減的情況。因此,晶體上各個晶面的指數一般限於簡單的整數。
 圖4
圖4晶體點陣中的每一組直線點陣可用記號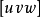 來表示,其中
來表示,其中 為三個互質的整數,記號為
為三個互質的整數,記號為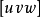 的直線點陣則與向量
的直線點陣則與向量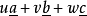 平行。例如
平行。例如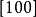 和
和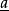 平行,
平行, 和
和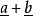 平行等。晶體上各個晶棱的記號和與其相應的直線點陣者同。在晶棱的記號
平行等。晶體上各個晶棱的記號和與其相應的直線點陣者同。在晶棱的記號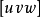 中,
中, 一般為簡單的整數。
一般為簡單的整數。
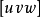

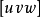
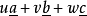
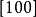
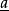

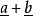
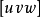

 圖5
圖5晶體上每一組與一通過晶體中心的假想直線平行的晶面形成一晶帶,晶帶中各對晶面間的交線亦必與上述假想直線平行,而後者一般稱為帶軸,晶帶或帶軸的記號與相應的晶棱者互相通用,若晶面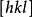 屬於晶帶
屬於晶帶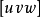 ,則
,則