有效質量係數

有效質量係數是指每個質點質量與其在某一振型中相應坐標乘積之和與該振型的主質量（或者說該模態質量）之比，即為該振型的有效質量係數。

基本介紹

• 中文名：有效質量係數
• 外文名：effective mass coefficient
• 所屬領域：建築科學

概述

一階振型自振頻率最小(周期最長),二階,三階....振型的自振頻率逐漸增大. 地震力大小和地面加速度大小成正比,周期越長加速度越小,地震力也越小。 自振振型曲線是在結構某一階特徵周期下算得的各個質點相對位移(模態向量)的圖形示意.在形狀上如實反映實際結構在該周期下的振動形態.振型零點是指在該振型下結構的位移反應為0。 振型越高，周期越短，地震力越大，但由於我們地震反應是各振型的疊代，高振型的振型參與係數小。 特別是對規則的建築物，由於高振型的參與係數小，一般忽略高振型的影響。

特性

振型的有效質量：這個概念只對於串連剛片系模型有效(即基於剛性樓板假定的，不適用於一般結構。）。某一振型的某一方向的有效質量為各個質點質量與該質點在該一振型中相應方向對應坐標乘積之和的平方。一個振型有三個方向的有效質量，而且所有振型平動方向的有效質量之和等於各個質點的的質量之和，轉動方向的有效質量之和等於各個質點的轉動慣量之和。

有效質量係數：如果計算時只取了幾個振型，那么這幾個振型的有效質量之和與總質量之比即為有效質量係數。這個概念是由WILSON E.L. 教授提出的，用於判斷參與振型數足夠與否，並將其用於ETABS程式。

振型參與質量：某一振型的主質量（或者說該模態質量）乘以該振型的振型參與係數的平方，即為該振型的振型參與質量。

振型參與質量係數：由於有效質量係數只適用於剛性樓板假設，不少結構因其複雜性需要考慮樓板的彈性變形，因此需要一種更為一般的方法，不但能夠適用於剛性樓板，也應該能夠適用於彈性樓板。出於這個目的，我們從結構變形能的角度對此問題進行了研究，提出了一個通用方法來計算各地震方向的有效質量係數即振型參與質量係數，規範即是通過控制有效質量振型參與質量係數的大小來決定所取的振型數是否足夠。（見高規（5.1.13）、抗規(5.2.2)條文說明）。這個概念不僅對糖葫蘆串模型有效。一個結構所有振型的振型參與質量之和等於各個質點的質量之和。如果計算時只取了幾個振型，那么這幾個振型的振型參與質量之和與總質量之比即為振型參與質量係數。

由此可見，有效質量係數與振型參與質量係數概念不同，但都可以用來確定振型疊加法所需的振型數。

我們注意到：ETABS6.1中，只有有效質量係數（effective mass ratio）的概念，而到了ETABS7.0以後，則出現了振型質量參與係數（modal participating mass ratio），可見，振型參與質量係數是有效質量係數的進一步發展，有效質量係數只適用於串連剛片系模型，分別有x方向 、y方向、rz方向的有效質量係數。振型參與質量係數則分別有x、y、z、rx、ry、rz六個方向的振型參與質量係數。

注釋

1）這裡的“質量”的概念不同於通常意義上的質量。離散結構的振型總數是有限的，振型總個數等於獨立質量的總個數。可以通過判斷結構的獨立質量數來了解結構的固有振型總數。具體地說：

每塊剛性樓板有三個獨立質量Mx,My,Jz；

每個彈性節點有兩個獨立質量mx,my；

根據這兩條，可以算出結構的獨立質量總數，也就知道了結構的固有振型總數。

2）若記結構固有振型總數是NM，那么參與振型數最多只能選NM個，選參與振型數大於NM是錯誤的，因為結構沒那么多。

3）參與振型數與有效質量係數的關係：

3-1)參與振型數越多，有效質量係數越大；

3-2)參與振型數 =0 時，有效質量係數 =0

3-3)參與振型數 =NM 時，有效質量係數 =1.0

4） 參與振型數 NP 如何確定？

4-1）參與振型數 NP 在 1-NM 之間選取。

4-2）NP應該足夠大，使得有效質量係數大於0.9。

有些結構，需要較多振型才能準確計算地震作用，這時尤其要注意有效質量係數是否超過了0.9。比如平面複雜，樓面的剛度不是無窮大，振型整體性差，局部振動明顯的結構，這種情況往往需要很多振型才能使有效質量係數滿足要求。

有效質量係數不滿足要求的原因分析和處理

在SATWE軟體的套用中，經常有設計人員會遇到某些工程在採用“總剛模型”進行設計時，結構有效質量係數總不滿足要求。增加振型數後，結構有效質量係數變化並不明顯，但採用“側剛模型”計算時卻較容易滿足要求。在此，擬結合具體的工程實例，與廣大設計人員探討產生結構有效質量係數不滿足要求的主要原因及處理方法。

工程概況

某工程為框架結構，共六層。其中第6層層高為4600mm，並在①～⑥、⑥～⑧、⑬～⑭之間的框架部分高度為3600mm。結構三維軸側圖如圖1所示；

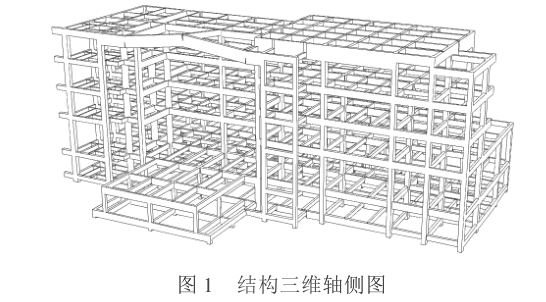圖1

第2、4、6層結構平面圖，見圖2a、2b和2c所示。

圖2

計算分析

本工程在不同計算振型數下結構有效質量係數的計算結果如表1所示。

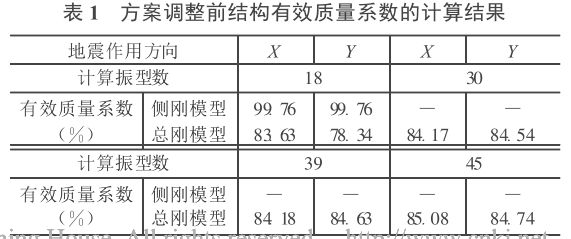表1

根據表1可知，該工程採用“側剛模型”計算時，在18個振型下，結構在X、Y向的有效質量係數均大於90%，滿足規範要求。但當採用“總剛模型”計算時，18個振型所計算出的在X、Y向的有效質量係數均不滿足要求。隨著振型數的增加，有效質量係數有所提高，但提高得非常有限。當振型數達到45個時，與18個振型相比，X向的有效質量係數僅提高了1.1%，Y向的有效質量係數僅提高了6.4%。是什麼原因使結構有效質量係數增長較慢呢？擬對上述計算結果進行分析。

(1)從圖1、2可以看出，此結構第六層存在局部錯層，錯層高度為1m。設計人員在採用PMCAD軟體進行結構建模時，對錯層部分採用的是“降節點高”的方式實現的。雖然本工程的錯層部分存在樓板，但由於採用了“降節點高”，使SATWE軟體在處理錯層部分的框架結構時，忽略樓板對框架結構的約束，並將錯層部分的節點定義為彈性節點，從而使結構自由度數大為增加。

(2)當採用“側剛模型”計算時，相當於採用了剛性板假定。每個樓層均只有三個自由度，六層結構共有十八個自由度。眾所周知，結構的振型數不能超過有質量貢獻的結構自由度總數。而十八個振型正好是剛性板假定下本工程的結構自由度總數，因此結構有效質量係數能夠滿足要求。

(3)當採用“總剛模型”計算時，由於前述彈性節點的大量存在，從而使結構自由度數大為增加，振型數也應該相應增加。對於本工程，結構有效質量係數增加得很慢的主要原因是由於彈性節點引起的局部振動所造成的。如圖3和圖4所示。

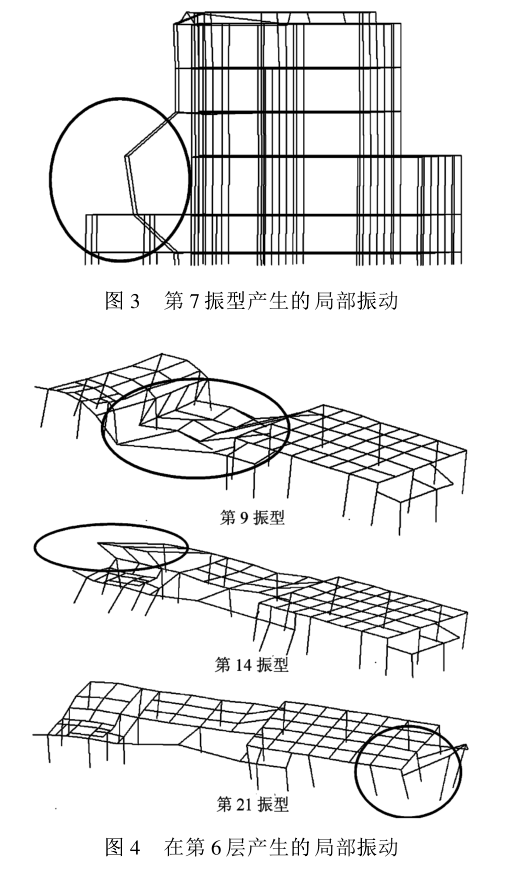圖3和圖4

圖3顯示，第7振型產生的局部振動主要是由於該工程存在單榀局部越層框架部分(見圖2所示)，該部分沿橫向在第2、3層越層高度達7900mm，沿縱向在2、3、4、5層越層高度達15100mm。由於這部分框架與主體結構聯繫非常薄弱，因此在高階振型作用下較易產生局部振動。

圖4表明，由於程式忽略了樓板對框架結構的約束作用，形成了許多彈性節點，從而在高階振型作用下產生了較多的局部振動。

方案調整

(1)由於單榀局部越層框架結構只是為了建築造型而設定，從結構的角度上分析並沒有太大意義。因此經與建築專業協商，改由建築師採用輕質材料達到立面效果，而結構專業則在結構設計時不考慮這部分框架結構。

(2)為近似考慮樓板對框架結構的約束作用,可採用輸入水平支撐的方式模擬樓板的剛度(如圖5所示)。

圖5

(3)通過對結構方案進行上述調整後，在高階振型作用下結構的局部振動得到了明顯的改觀，採用SATWE軟體的“總剛模型”進行設計時，在27個振型下，結構有效質量係數X向為99.62%，Y向為91.69%，滿足要求。

(4)本工程也可以採用另一有效方案使有效質量係數滿足要求，就是將第六層在SATWE軟體“特殊構件補充定義”中，全層定義為“彈性膜”，然後採用“總剛模型”進行設計，在36個振型下，結構有效質量係數X向為99.30%，Y向為92.55%，滿足要求。

(5)需要說明的是，雖然通過方案調整使結構的局部振動得到了明顯的改善，結構有效質量係數滿足要求，但由於受結構方案本身的限制，在高階振型作用下仍然存在一定的局部振動。對於這些產生局部振動的部位，設計人員應給予一定的重視。

(6)雖然本工程即便不經過方案調整，繼續加大振型數，最終也能實現有效質量係數滿足要求，但對應於高階振型所產生的局部振動，設計人員不宜忽視。