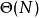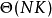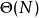基本介紹
- 中文名:最長公共子串列
- 外文名:Longest common subsequence
- 本質:尋找兩個或多個字元串最長的子串
- 套用:計算機科學
樣例,問題定義,求解算法,
樣例
字元串"ABABC","BABCA"以及"ABCBA"的最長公共子串是"ABC"。其他的公共子串包括"A"、"AB"、"B"、"BA"、"BC"以及"C"。
ABABC
|||
BABCA
|||
ABCBA
問題定義
給定兩個字元串,長度為 的字元串
的字元串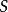 以及長度為
以及長度為 的字元串
的字元串 ,求最長的子串
,求最長的子串 同時是
同時是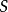 以及
以及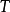 的連續子串。
的連續子串。

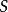



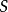
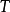
問題可以一般化為k-公共子串問題——給定字元串的集合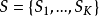 ,其中
,其中 ,
, 。對於滿足
。對於滿足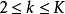 的
的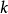 ,找出至少是
,找出至少是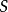 中
中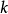 個字元串的公共子串的最長串。
個字元串的公共子串的最長串。
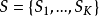


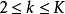
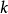
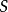
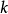
求解算法
利用廣義後綴樹,我們可以在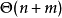 的時間複雜度內求出
的時間複雜度內求出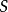 和
和 的最長公共子串的長度和他們的起始位置。而如果利用動態規劃求解,則時間複雜度為
的最長公共子串的長度和他們的起始位置。而如果利用動態規劃求解,則時間複雜度為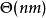 。而對於一般化的公共子串問題,使用動態規劃的求解的時間複雜度為
。而對於一般化的公共子串問題,使用動態規劃的求解的時間複雜度為 ·...·
·...·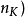 ,利用廣義後綴樹則需
,利用廣義後綴樹則需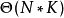 的時間複雜度。
的時間複雜度。
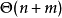
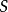

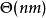

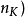
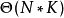
利用廣義後綴樹
字元串集合的最長公共子串可以通過構造一棵廣義後綴樹, 然後去查找擁有來自所有集合中字元串的葉節點的最深的內部節點來得到。圖一展示了字元串“ABAB”,“BABA”和“ABBA”對應的廣義後綴樹。為了方便後綴樹的構造和區分字元串,每個串的結尾都添加了終結符“$”和字元串編號,分別變成了“ABAB$0”,“BABA$1”和 “ABBA$2”。如圖所示,串“A”,“B”,“AB”和“BA”的節點對應的子樹都包含來自所有字元串的葉節點。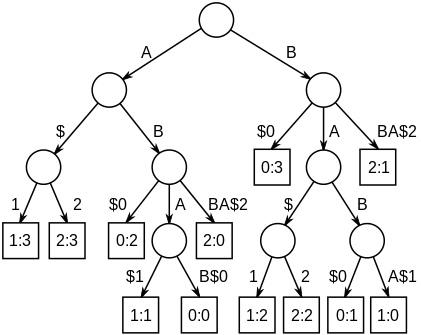 圖一
圖一
 圖一
圖一假定字母表的大小是常數,構造這樣的一顆後綴樹的時間複雜度為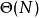 。這樣,如果將整個樹自頂向上遍歷,並在每個節點通過一個位向量標記每個節點的子樹中出現過的所有字元串的,則k-公共子串問題可以以
。這樣,如果將整個樹自頂向上遍歷,並在每個節點通過一個位向量標記每個節點的子樹中出現過的所有字元串的,則k-公共子串問題可以以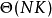 的時間複雜度來解決。特別地,如果後綴樹為常數時間的最近公共祖先檢索做了最佳化,那么問題將可以在
的時間複雜度來解決。特別地,如果後綴樹為常數時間的最近公共祖先檢索做了最佳化,那么問題將可以在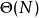 的時間複雜度內解決。
的時間複雜度內解決。