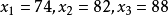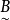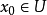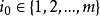最大隸屬原則

最大隸屬原則(maximum membership principle)是模糊數學的基本原則之一，它是用模糊集理論進行模型識別的一種直接方法，對於n個實際模型，可以表示為論域X上的n個模糊子集A₁，A₂，…，A_n，x₀∈X為一具體識別對象，如果有i₀≤n，使A_i0(x₀)=max(A₁(x₀)，A₂(x₀)，…，A_n(x₀))，則稱x₀相對隸屬於A_i0，這即是最大隸屬原則，在實際套用中，可以用來進行疾病診斷、機器故障診斷或進行癌細胞的識別等。

基本介紹

• 中文名：最大隸屬原則
• 外文名：maximum membership principle
• 所屬學科：數學
• 所屬問題：模糊集合論
• 簡介：模糊數學的基本原則之一

最大隸屬原則Ⅰ

最大隸屬原則Ⅰ 設論域上有m個模糊子集（即m個模型），構成一個標準模型庫，若對於任一，有，使得

則認為相對隸屬於。

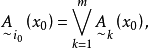
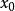
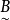【例1】學習成績的模糊識別 在論域（分數）上確定三個表示學習成績的模糊集=“優”，=“良”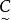，=“差”，當一位同學的數學成績為88分時，該同學的數學成績是評為優、良，還是差？

解 先建立模糊集的隸屬函式，用指派方法建立論域（分數）的的隸屬函式：

將代入隸屬函式計算，得

根據最大隸屬原則Ⅰ，該同學的數學成績相對於三個模型應隸屬於，可評為良。

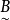
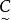
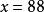
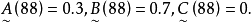
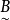
最大隸屬原則Ⅱ

最大隸屬原則Ⅱ 設論域上有一個標準模型，待識別的對象有n個，，如果有某個滿足

則應優先錄取。

【例2】學習成績的模糊識別 設論域（3個學生的英語成績），在U上定義一個模糊集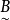=“良”，待識別的對象有3個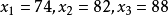：，仍選用例1中模糊集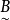=“良”的隸屬函式。

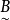
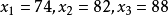
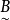
現將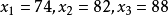分別代入計算，得

由於82分隸屬=“良”的程度最大，所以第二個學生的英語成績最靠近“良”。