詳細解釋
我們知道,一個事件的機率越大,它發生的可能性就越大。當面對未來情況的各種狀態時,由於已經知道它們出現的機率,或者這些機率可以估算出來,決策者就可以挑選其中機率最大狀態作為考慮問題的出發點,讓後在挑選對自己最有利的行動方案。
決策步驟
我們把用最大可能法進行決策的步驟歸納如下:
(1)明確問題的決策目標;
(2)明確未來狀態
及其機率,確定可供選擇的方案
;
(4)由未來狀態的機率與
(或R)從
中選出最佳行動方案。
損益函式
定義
損益函式
是一個關於兩個變數a,x的函式,其中第一個變數a表示決策者可以採取的各種方案;第二個變數x表示未來外界情況可能發生的各種狀態。
損益矩陣
把損益函式中的可能值按照一定的次序用矩陣形式表示出來,就得到了損益矩陣。損益矩陣可用大寫的英文字母R表示。損益矩陣是
風險型決策常用的分析手段之一,又稱“決策表”、“決策矩陣”、“益損表”、“風險矩陣”。
(1)損益矩陣的基本要素:
1.狀態變數:指可能影響
決策後果的各種客觀外界情況或自然狀態。是不可控因素。
2.決策變數:指
決策者所採取的各種行動方案,是可控因素。
4.損益值:在一種自然狀態下選取某種方案所得結果的損益值。
(3)損益矩陣的套用
損益矩陣由
備選方案、自然狀態(及其發生的
機率)益損值所組成。對
決策問題的描述就集中地表現在損益矩陣上,
決策分析就是以損益矩陣為基礎,運用不同的分析
標準與方法,從若干個可行方案中選出最優方案。
舉例
例1
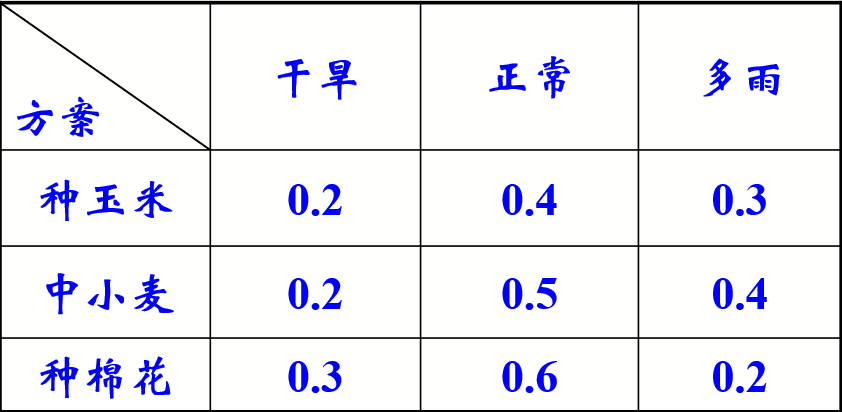
某農戶要在地里種一種農作物,它可以種玉米、小麥或棉花.根據歷年的氣象資料了解到天氣乾旱、天氣正常和天氣多雨的機率分別為0.3,0.6,0.1。這三種農作物在三種天氣狀態下獲利情況如下表所示,該農戶應該怎樣決策呢?
該用戶的目的是獲取最大利潤.未來天氣狀態正常的機率是0.6,遠大於乾旱年份的機率0.3和多雨的年份0.1,使用最大可能法進行決策,應該選定天氣正常作為考慮哪種農作物的出發點。
解:在天氣正常的年份里,由上表可知中間那一列棉花獲利最多(0.6萬元),該用戶的最佳行動方案是在這塊地里種棉花。
在這裡需要指出,該農戶決定中棉花,並不意味著他就能獲得0.6萬元的利潤,畢竟這是一個帶有風險的決策.運用機率的思想方法不難發現,雖然未來天氣多雨的機率只有百分之十,但是天有不測風雲,一旦降水量多的年份來臨,該農戶就只有0.2萬元,比種玉米和小麥的收入要少。即我們的預測可以最合理,但並不一定是最好!
例2
為生產某種產品,投資方有兩種投資方案,一個是建設大工廠,另一個是建設小工廠.大工廠需要投資300萬元,小工廠需要投資150萬元,兩者的使用期限都是10年.估計在此期間,產品暢銷的機率是0.7,產品滯銷的機率是0.3.兩個方案的年度收益情況如下表所示.投資方應該做出怎樣的決策呢?
兩個方案的年度收益情況單位:萬元。
解:投資方案的決策目標是獲取最大利潤.由於上表中給出的是一年的收益情況,為了討論方便,需要求出工廠投產10年的損益函式R(a,x)或損益矩陣R。
損益函式為:
損益矩陣為:
使用機率的記號,由題意,
P(產品暢銷)=0.7;P(產品滯銷)=0.3。
根據最大可能法,應與未來產品暢銷的狀態作為選擇基建方案的出發點。
從損益矩陣表示產品暢銷的第一列數據易見,早大工廠的總利潤700萬元遠大於造小工廠的總利潤250萬元,投資方應該採納造大工廠的基建方案。
進一步觀察益損矩陣R可以看出,造大工廠雖然可能獲得700萬元,但承擔的風險很大,一旦由於種種始料未及的原因產品滯銷,就要遭受損失500萬元.而若建設小工廠,不管產品暢銷、滯銷,均能獲利,但獲利的數量相對來說要小得多。這個例子表明
風險型決策在實際工作中有很大的套用價值。