最合適區域法

最合適區域法是日本田中教授在研究價值係數時提出的一種選擇價值工程(VE)目標的方法。基本思路是：價值係數相同的對象，由於各自的成本係數與功能評價係數的絕對值不同，因而對產品價值的實際影響有很大差異，在選擇目標時不應把價值係數相同的對象同等看待，而應優先選擇對產品實際影響大的對象。至於對產品影響小的，則可根據必要的功能，決定其選擇與否。根據價值係數選擇VE的目標，應該區別目標的成本係數和功能評價係數，大的要從嚴控制。不允許其價值係數對1的偏差過大，對於功能係數和成本係數小的目標，則可放寬控制，即使其對1偏差較大，也不列為VE的目標。這樣既可使VE能抓住少數對象開展工作，又不被對象過多所困擾，保證不漏掉重點。

基本介紹

• 中文名：最合適區域法
• 別稱：田中法
• 提出者：田中教授
• 提出時間：1973年
• 套用學科：價值係數法
• 適用領域範圍：精選價值工程對象、選擇價值工程改進

什麼是最合適區域法

最合適區域法是一種在價值係數法的基礎上利用一個最合適區域來精選價值工程對象、選擇價值工程改進對象的方法。

最合適區域法的運用

最合適區域法的原理與功能係數評價法是一致的，認為價值係數在1附近是合適的，可不作為改進對象。

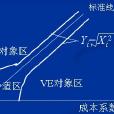
曲線內稱為最合適區，曲線外的對象皆為VE(價值工程)對象。

最合適區域法在選擇價值工程對象時，不僅僅考慮價值係數值大於1或小於1的情況，而且還要考察功能係數和成本係數絕對值的大小，從而對各對象加以區別對待。

在零部件價值係數相同的情況下，如果功能係數和成本係數的絕對值不同，那么它們對經濟效果的影響也不同。所以不能簡單地以價值係數來選擇價值工程對象，還應考慮各對象的功能係數和成本係數，對兩者較大的應作重點考慮，對兩係數較小的對象可不作重點考慮或不考慮。

最合適區域法的基本思想

其基本思想是：對於那些功能重要性係數和實際成本係數較大的零件，由於它們改善功能或降低成本的潛力大，對全局的影響大，應當從嚴控制，不應偏離價值係數標準線(Vi = 1)太遠，即當價值係數對1稍有偏離時，就應選作重點對象；而對於那些功能重要性係數和實際成本係數較小的零件，因其對全局影響小，功能改善或成本降低的潛力不大，可從寬控制，允許偏離Vi = 1的價值係數標準線遠一些。