最優抽樣比是誤差最小而抽樣經費開支最省的抽取比。抽樣誤差隨抽樣數的增加而減小,而經費開支隨抽樣數增加而增加,兩者是相互制約的。在實施抽樣時,通常很難同時滿足這兩個條件,合理的做法是在給定的經費條件下使抽樣誤差最小,或者,在給定抽樣誤差的條件下使抽樣費用最省。
基本介紹
- 中文名:最優抽樣比
- 外文名:optimal sampling ratio
- 套用學科:數學術語
- 範疇:數理科學
- 定義:誤差最小而抽樣經費開支最省
- 涉及:抽樣誤差
概述
最優抽樣比方法




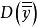










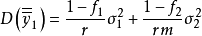






















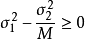

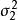



最優抽樣比是誤差最小而抽樣經費開支最省的抽取比。抽樣誤差隨抽樣數的增加而減小,而經費開支隨抽樣數增加而增加,兩者是相互制約的。在實施抽樣時,通常很難同時滿足這兩個條件,合理的做法是在給定的經費條件下使抽樣誤差最小,或者,在給定抽樣誤差的條件下使抽樣費用最省。




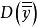










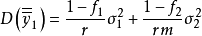






















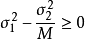

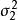


最優抽樣比是誤差最小而抽樣經費開支最省的抽取比。抽樣誤差隨抽樣數的增加而減小,而經費開支隨抽樣數增加而增加,兩者是相互制約的。在實施抽樣時,通常很難同時...
隨機抽樣優缺點 編輯 隨機抽樣優點 單純隨機抽樣有不少優點,主要有:第一,單純隨機抽樣方法簡單、直觀,是隨機抽樣理論中最基本的組織形式,是抽樣理論的基石。例如,...
1 基本介紹 2 序貫似然比檢驗 最優序貫檢驗基本介紹 編輯 序貫檢驗(sequential test)是指基於序貫抽樣觀測結果,運用序貫分析方法的統計假設檢驗。區分兩個統計假設H0...
等距抽樣優缺點 編輯 等距抽樣方式相對於簡單隨機抽樣方式最主要的優勢就是經濟性。等距抽樣方式比簡單隨機抽樣更為簡單,花的時間更少,並且花費也少。使用等距抽樣...
方便抽樣優缺點 編輯 優點:容易實施,調查的成本低。缺點:樣本單位的確定帶有隨意...方便抽樣的最大特點是容易實施,調查成本低,因此,方便樣本無法代表有明確定義的...
配額抽樣優缺點 編輯 配額抽樣優點 適用於設計調查者對總體的有關特徵具有一定的了解而樣本數較多的情況下,實際上,配額抽樣屬於先“分層”(事先確定每層的樣本量)...
4.9分層隨機抽樣的精度研究1914.9.1分層隨機抽樣與簡單隨機抽樣精度比較1914.9.2最優分配在精度上的改進1934.9.3分層隨機抽樣精度反比簡單隨機抽樣差的情況194...
(3)最優分配法,即各層抽得的樣本數與所抽得的總樣本數之比等於該層方差與各類方差之和的比。[3] 抽樣方法優點 (1)減小抽樣誤差,分層後增加了層內的同質...
貨幣單位抽樣最基本的特徵是把總體中的單元貨幣單位作為抽樣單位,每個貨幣單位被選中...貨幣單位抽樣法優缺點 編輯 1、優點1)貨幣單位抽樣法繼承了屬性抽樣的統計分析...
任意抽樣是非機率抽樣中最簡便、費用和時間最節省的一種方法。但是,如果總體中...任意抽樣優缺點 編輯 任意抽樣技術簡便易行,可以及時取得所需的資料,節約時間和...
機率抽樣優缺點 編輯 ⑴ 機率抽樣包括以下幾個方面的優點:調查者可獲得被抽取的...簡單隨機抽樣是一種廣為使用的機率抽樣方法。是最完全的機率抽樣。如前面提到的...
分層隨機抽樣,又稱類型隨機抽樣,它是先將總體各單位按一定標準分成各種類型(或層);然後根據各類型單位數與總體單位數的比例,確定從各類型中抽取樣本單位的數量;...
多重抽樣優缺點 編輯 多重抽樣的最大優點是可以在一套樣本中,根據對調查標誌的不同要求,進行幾個大小不同樣本的調查,便於組織和節約費用;但缺點是抽樣誤差較大[...
分層隨機抽樣中,各層中每個單位費用一樣(即Ch=C)時樣本單位的最優分配方法。內曼分配是一種不等機率樣本設計,每個元素的抽樣機率取決於其所在層的元素個數和樣本...
4 優缺點 5 誤差 6 取樣的分類 ▪ 隨機抽樣法 ▪ 非隨機抽樣法 聚類...相對於簡單隨機抽樣方式,系統抽樣最主要的優勢就是經濟性。等距抽樣方式比簡單...
