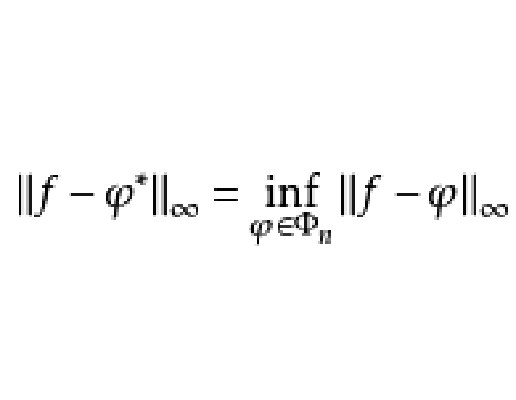最佳逼近廣義多項式(generalized polynomials of best approximation)是指達到最佳逼近的廣義多項式,Haar提出了最佳逼近廣義多項式的惟一性定理。
基本介紹
- 中文名:最佳逼近廣義多項式
- 外文名:generalized polynomials of best approximation
- 所屬學科:數學
- 所屬問題:實變函式逼近論
- 相關概念:最佳逼近、廣義多項式等
基本介紹,最佳一致逼近問題,最佳一致逼近多項式,切比雪夫定理,最佳(一致)逼近廣義多項式,哈爾條件,充要條件,唯一性定理,
基本介紹
最佳一致逼近問題
在次數不超過n的多項式集合 中求
中求 ,使它與
,使它與 的誤差
的誤差





最佳一致逼近多項式
給定 ,若存在
,若存在 ,使
,使








理論上已證明,對任何 ,都存在惟一的
,都存在惟一的 ,使式(1)成立,實際上在集合
,使式(1)成立,實際上在集合 中每一元素,
中每一元素, 都對應一個偏差
都對應一個偏差 ,由於
,由於 ,故集合
,故集合 有下界,從而有下確界
有下界,從而有下確界 。如果存在
。如果存在 使
使 就是所要求的最佳一致逼近多項式。切比雪夫(Chebyshev)對最佳一致逼近多項式的特性,給出了下面的重要定理。
就是所要求的最佳一致逼近多項式。切比雪夫(Chebyshev)對最佳一致逼近多項式的特性,給出了下面的重要定理。










切比雪夫定理
設 是
是 在[a,b]上的最佳一致逼近多項式的充分必要條件是,
在[a,b]上的最佳一致逼近多項式的充分必要條件是, 在[a,b]上至少有
在[a,b]上至少有 個點
個點






這個定理表明,最佳一致逼近多項式 的特性,即
的特性,即 逼近
逼近 的誤差分布是均勻的,如圖1所示。
的誤差分布是均勻的,如圖1所示。



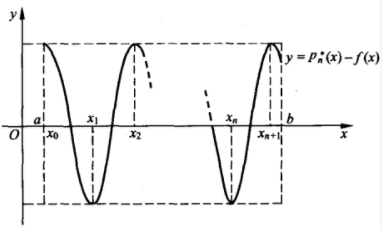 圖1
圖1最佳(一致)逼近廣義多項式
若在空間 中取子集
中取子集 ,若存在
,若存在 使
使










哈爾條件
函式 線性無關,若子集
線性無關,若子集 中任一不恆為零的廣義多項式,即
中任一不恆為零的廣義多項式,即





顯然,子集 是滿足哈爾條件的。
是滿足哈爾條件的。

充要條件
有了上述哈爾條件的定義,就可類似定理切比雪夫定理得到下面定理。
定理若子集 滿足Haar條件則對任意給定的函式
滿足Haar條件則對任意給定的函式 ,使廣義多項式
,使廣義多項式








唯一性定理
Haar還提出了下面的最佳逼近廣義多項式的惟一性定理。
定理 對任何函式 ,子集
,子集 中存在惟一的最佳逼近廣義多項式的充分必要條件是子集
中存在惟一的最佳逼近廣義多項式的充分必要條件是子集 滿足Haar條件。
滿足Haar條件。