曼德勃羅特集(Mandelbrot set),簡稱M集. 由曼德勃羅特(Mandelbrot , B. B.)提出的一類分形集。
概念提出,推論,
概念提出
曼德勃羅特集是在複平面上按進行疊代,對應於一定的C值,在n~二時,所有Z
不趨於二的Z。
推論
點的邊界構成了朱利亞集(參看“朱利亞集”).從計算機模擬中還發現,參數C的微小變化都會造成朱利亞集形狀的顯著改變.在各種C 值對應的朱利亞集中,有些是離散的,有些是連通的.如果在複平面上將對應於連通的朱利亞集的C 點塗黑,而把對應於離散的朱利亞集的C點塗白,就會得到如下圖所給出的點集.圖中的黑色部分所代表的點集就是M集,邊上的圖形就是相應的M 集中各種點C的朱利亞集.
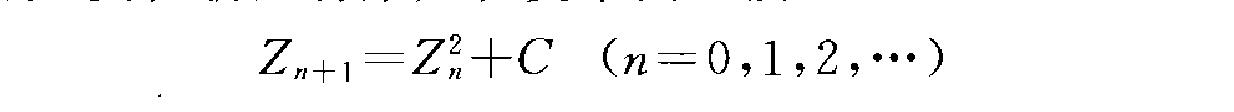

在複平面上將C值固定,而讓Z作為原始點進行疊代變化,就可得到朱利亞集.所以,對應於選定不同C值的朱利亞集有無窮多個,而M集只有一個.如果把M集的邊界放大,便會顯示出M集下無窮盡的微型縮影.這些微型M集與母集相似但並不完全一樣.M集的這種結構體現了分形幾何的特點,即局部與整體的相似性.這個性質與朱利亞集是一致的.現在數學上已證明M集是連通的,即便看起來像是懸浮在平面上的M集也是通過細線同母集連結在一起的.從某種意義上說,M集概括了所有可能的朱利亞集,因此常把M集看成是朱利亞集的圖象存貯器.有關M集的性質仍是數學家們的一道難題.
