基本介紹
- 中文名:曼代爾-克雷爾效應
- 外文名:Mandel-Cryer effect
- 學科:土力學
- 發現者:曼代爾、克雷爾
- 現象:固結初期超靜孔隙水壓力是否消散
- 有關術語:超靜孔隙水壓力
簡介,比奧固結理論,超靜孔隙水壓力,
簡介
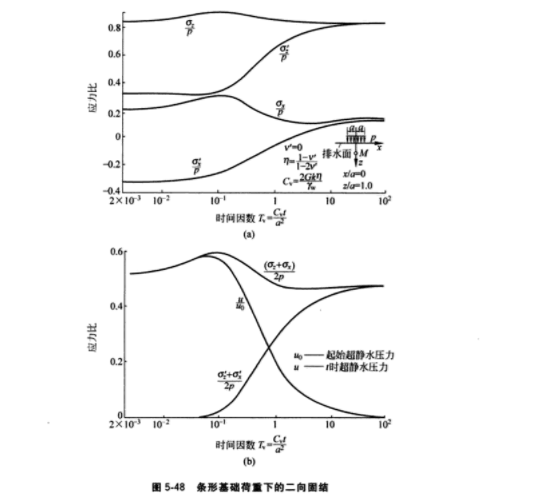
用比奧理論解飽和土的固結問題時出現一種異乎尋常的現象:在不變的荷重施加於土體上以後的某段時間,土體內的孔隙水壓力不是下降,而是繼續上升,而且超過應有的壓力值。該現象先後由曼代爾和克雷爾發現,故稱曼代爾-克雷爾效應,或稱為應力傳遞效應。產生曼代爾-克雷爾效應的原因可以解釋如下。在表面透水的地基面上施加荷重,經過短暫的時間,靠近排水面的土體由於排水發生體積收縮,應力與有效應力均有增加。土的泊松比也隨之改變。但是內部土體還來不及排水,為了保持變形協調,表層土的壓縮必然擠壓土體內部,使那裡的應力有所增大。因此,某個區域內的總應力分量將超過它們的起始值,而內部孔隙水由於收縮力的壓迫,其壓力降上升。水平總應力分量的相對增長(與起始值相比)比垂直分量的相對增長要大。淺部土層距離排水面較近,超孔壓消散較快,深部土層超孔壓消散緩慢,並產生了曼代爾-克雷爾效應。
按平面應變問題分析,該效應有以下特點:地面排水性能愈差,該效應愈不顯著,地面不透水時,幾乎無該效應。如果地面透水,超靜水壓力出現峰值點的時間隨深度而推後,並且峰值愈來愈高。由於曼代爾-克雷爾效應,地面透水的土體中一點的剪應力隨時間變化,最大值可能在固結過程中的基礎邊緣產生。
比奧固結理論
太沙基固結理論只在一維情況下是精確地,對二維、三維問題並不精確。比奧(Biot)從較嚴格的固結機理出發推導了準確反映孔隙壓力消散與土骨架變形相互關係的三維固結方程,一般稱為真三維固結理論,而將太沙基三維方程稱為擬三維固結方程。比奧(M.A.Biot)於1941年創立的三維固結理 論。該理論將彈性理論求解土體的應力和變形的方 法與滲透水流連續條件相結合,建立由四個偏微分 方程所組成的固結方程組,可同時求解土體在固結 過程中任意點的孔隙水壓力和變形。常稱為真固結 理論。其求解非常複雜,一般需用數值法並藉助於電子計算機。太沙基-倫杜列克擴散方程,又稱太沙基-倫杜列克固結理論,該理論與太沙基一維固結理論建立在同一個理論基礎上,即在飽和粘土的固結過程中,土中任意單元體的體積變化率與流經單元體表面的水量變化率相等。在其推導過程中,只考慮了水流連續條件和彈性的應力應變關係,而沒有涉及土體變形的幾何條件,這種理論又被稱為準多維固結理論。可以利用差分法求解。
超靜孔隙水壓力
由外荷載引起的孔隙水壓應力,稱為超靜孔隙水壓應力。超靜孔隙水壓應力將會隨著時間而消散,所以超靜孔隙水壓應力是時間的函式。超靜孔隙水壓應力稱為附加孔隙水壓應力更為合適,在載入瞬時為最大,當固結度達到100%時為零。超靜孔隙水壓應力是由土體的體積變化趨勢引起的,也就是說,超靜孔隙水壓應力是土的體積變形性質在不排水條件下的表現。這意味著土體的體積變形性質(壓縮性和剪脹性)在不同的排水條件下有不同的表現。它在排水情況下表現為體積變化,而在不排水條件下則表現為超靜孔隙水壓應力變化。
超靜孔隙水壓力(excess pore water pressure)是由土的變形趨勢引起的孔隙水壓力,也就是說,土體本應發生應變,但由於一時排水受阻,土中產生孔隙水壓力,使作用於土骨架上的有效應力發生變化,從而限制其變形。超靜孔隙水壓力往往伴隨著滲流和固結。超靜孔隙水壓力是由於外部作用或者邊界條件變化在土體中引起的不同於靜孔隙水壓力的那部分孔隙水壓力,在有排水條件下,它將逐漸消散,並在消散過程中伴隨土體的體積變化。