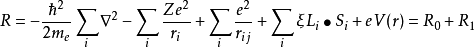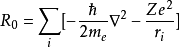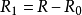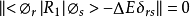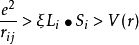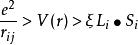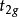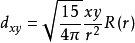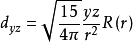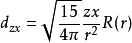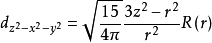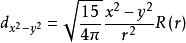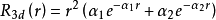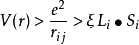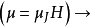晶體場效應

晶體場理論是計算離子能級的一種有效方法，在物理，化學，礦物學，雷射光譜學以及順磁共振中有廣泛套用。

基本介紹

• 中文名：晶體場效應
• 外文名：Crystal-Field Effect

基本思想

認為中心離子的電子波函式與周圍離子（配位子）的電子波函式不相重疊，因而把組成晶體的離子分為兩部分：基本部分是中心離子，將其磁性殼層的電子作量子化處理；非基本部分是周圍配位離子，將其作為產生靜電場的經典處理。配位子所產生的靜電場等價為一個勢場——晶體場。

晶體中的晶體場效應

a.晶體場對磁性離子軌道的直接作用引起能級分裂使簡併度部分或完全解除，導致軌道角動量的取向處於被凍結狀態。

b.晶體場對磁性離子自旋角動量的間接作用。通過軌道與自旋耦合來實現。常溫下，晶體中自旋是自由的，但軌道運動受晶體場控制，由於自旋－軌道耦合和晶體場作用的聯合效應，導致單離子的磁各向異性。

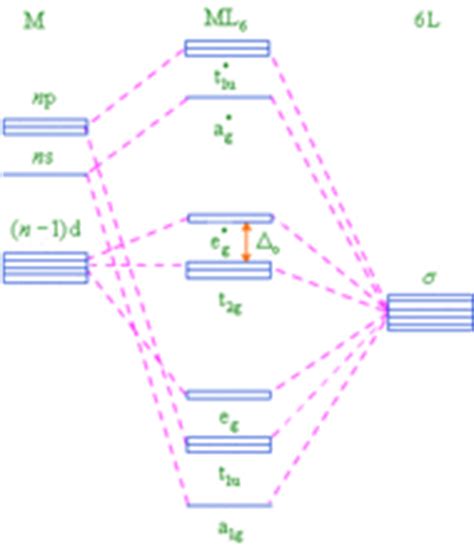
晶體場劈裂作用

考慮到晶體場與L-S 耦合作用，晶體系統的哈密頓量為：

等式中間第一項為第i個電子的動能，第二項為電子勢能，第三項為原子內電子的庫侖相互作用，第四項為S-L軌道相互作用，第五項為中心離子與周圍配離子產生的晶場間相互作用。

(微擾哈密頓量)

採用簡併態微擾法可計算系統的微擾能量，為此，須求解方程：

1. 弱晶場

與自由原子（離子）一樣，滿足洪特規則。

稀土金屬及其離子屬於此

2. 中等晶場

仍滿足洪特規則，但晶體場V(r)首先對軌道能量產生影響，即能級分裂，簡併部分或完全消除。

含3d電子組態的離子的鹽類屬於此

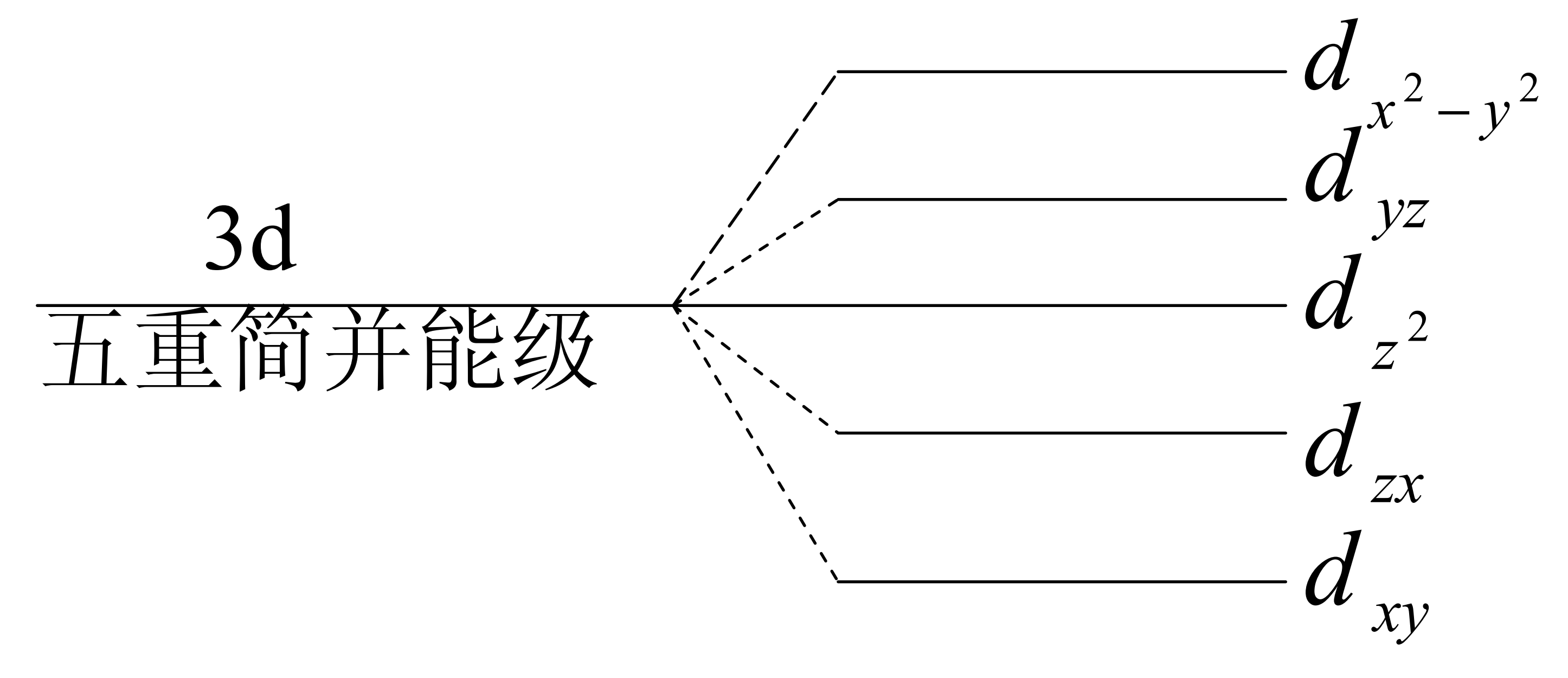
對於3d電子， l=2，角動量可有2l+1 =5個不同取向，由此形成五重簡併能級如下（能量由n決定）：

項（三重簡併）

e_g(2)項

註： R(r)為歸一化的徑向波函式

選用Richardson等人的近似， Hartfree-Fock解析波函式：

使3d電子的簡併能級分裂的方法：
a. 外加磁場
不同取向的角動量對應不同的磁矩（大小、方向） 不同的磁矩對確定方向的H有不同的位能 磁場使原來簡併的能級分裂為五個不同的能級。

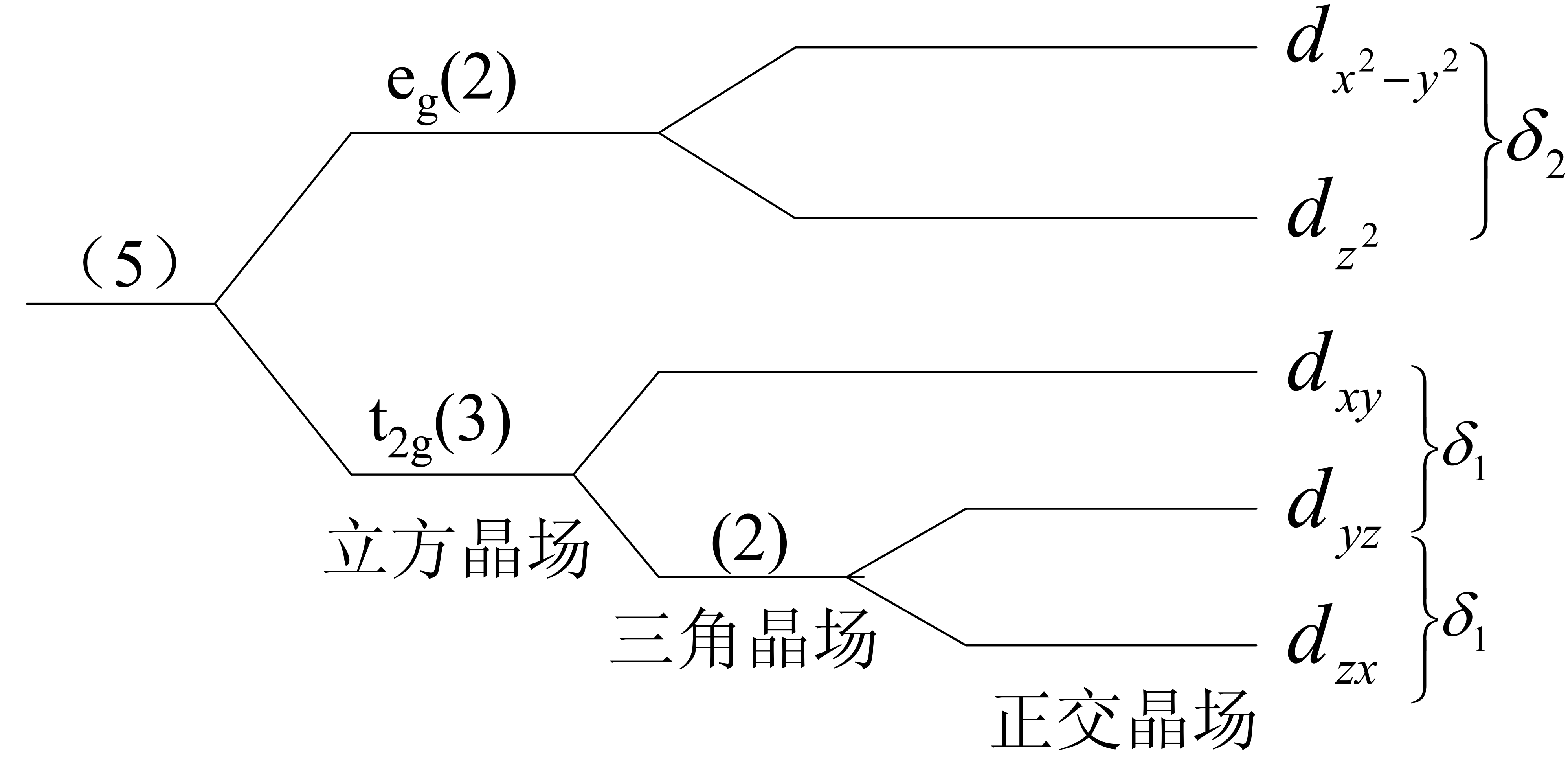
b. 將3d電子置於晶場中

由於e_g的兩個軌道正對近鄰離子，而t_2g的三個軌道指向兩個近鄰離子的間隙區域，因而有能級間能量差關係為δ₁<< δ₂。

3d電子五重簡併能級在晶場的作用下依順序發生能級分裂，在占據這些能級的電子中，當存在簡併能級中的電子不均勻分布時，有時晶體會自發地發生畸變，對稱性變低，軌道的簡併被解除，使電子占有的能級變得更低——楊特勒效應（Jahn-Teller Effection） 。
例如：Cu2+(3d⁹)，置於正八面體晶體中，電子組態為： t_2g⁶e_g³

考慮d¹⁰電子組態，其電子云呈球形對稱。去掉一個d_x²_-y²電子 (t_2g6)(d_z²)2(d_x²_-y²)（這種狀態在x與y軸方向，電子出現幾率小） Cu2+原子核內正電荷在x-y軸方向所受禁止較小 從而Cu²⁺原子核吸引位於x-y軸方向的近鄰異性離子能力較強，而在z軸較弱 Cu²⁺周圍點陣發生畸變， 其近鄰離子所構成的八面體變為沿z軸伸長的八面體。此時在e_g中d_z²能量比d_x2-y2低，而在t_2g中d_zx<d_yz<d_xy。

同理，若將d¹⁰去掉一個d_z²電子，則正八面體將畸變為沿z軸收縮的八面體。此時， e_g中能量d_x2-y2< d_z2-x2-y2， t_2g中：d_xy<d_yz<d_zx。

由於δ₁<< δ₂，當Cu²⁺的周圍點陣由正八面體對稱疇變成為伸長或收縮的八面體對稱時， t_2g⁶狀態的能量未變，而三個e_g電子的能量降低。 晶場畸變後Cu²⁺能量降低了——產生畸變的原因（楊特勒效應的機理）。

軌道角動量的凍結

由於晶場劈裂作用，簡併能級出現分裂，可能出現最低軌道能級單態，當單態是最低能量的軌道時，總軌

道角動量絕對值 L²雖然保持不變，但是其分量L_z不再是運動常量。
當L_z的平均值為零，即 時，就稱為軌道角動量的凍結。一個態的磁矩是磁矩=(L_z+2S_z) μ ，當L_z的平均值
為零時，對於整個磁性，軌道磁矩不作貢獻。（單態簡併度為1（簡併度由2l+1決定)簡併度解除2l+1=1。所以l=0時為單態。）離子的軌道角動量凍結程度取決於軌道簡併度解除的程度。

3. 強晶場

不滿足洪特規則，導致低自旋態。
發生於共價鍵晶體和4d，5d，6d等過渡族化合物。