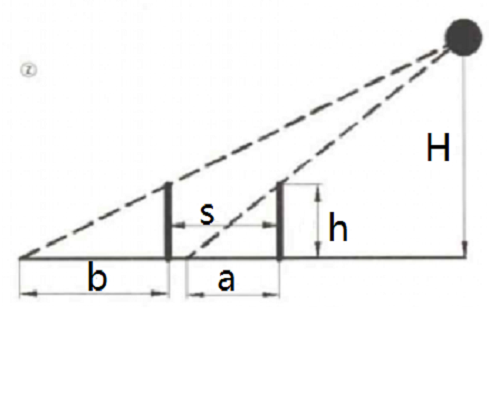
趙爽在給《周髀算經》寫注的時候,提出了測量太陽高度的想法。假定大地是平的(這也是合理的,因為趙爽的兩次測量之間相距不過幾十或幾百米),在平地上立兩表(表就是“桿”的意思),高度相等(或一個表用兩次也可),設為h。兩表一前一後,距離為s,且與目標(此處是太陽) 在同一平面內。前面的表(即離目標近的表) 的影子長度為a,後面的影子長度為b。利用相似原理,容易計算出日高H為H=h(1+s/(b-a))(即:日高= (表高×表距)/影差+表高)。但是,這一 方法儘管在理論上可行,其實是無法測出太陽真實高度的,因為H太大了,a 與b幾乎相等,而且表的任何輕微晃動所造成的誤差,都將遠超過b 與a的真值之差。因此,這個“日高公式”在理論上是正確的,在實踐上卻是不可行的。
基本介紹
- 中文名:日高公式
- 所屬學科:地理、數學
- 相關著作:《周髀算經》
- 相關人物:趙爽、吳元俊等
公式記載,日高公式的證明,海島公式,
公式記載
根據《周髀算經》,周公測日的方法大致是這樣的:先後兩次測量同一圭表在不同處的日影長,然後用下面公式算出日高:
日高= (表高×表距)/影差+表高.
 圖1趙爽測量太陽高度想法示意圖
圖1趙爽測量太陽高度想法示意圖在平地上立兩表(表就是“桿”的意思),高度相等(或一個表用兩次也可),設為h。兩表一前一後,距離為s,且與目標(此處是太陽) 在同一平面內。前面的表(即離目標近的表) 的影子長度為a,後面的影子長度為b。
日高公式的證明
日高公式怎么來的? 《周髀算經》沒有說.趙爽為《周髀算經》作注時,畫了一幅“日高圖”並附有圖說,實際是對日高公式的證明。趙爽原圖已佚失,根據殘存但是原始的信息,利用《九章算術》中經常出現的“出人相補”原理,吳元俊復原了趙爽的“日高圖”,並補出了日高公式的證明。
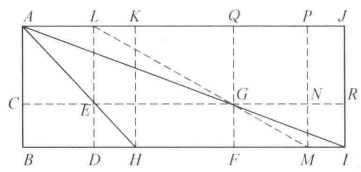 圖2
圖2其中三角形△ABI 全等於△AJI,△ACG 全等於△AQG,而△FGI 全等於△GRI。根據“出人相補”原理,應有
△AJI 的面積一(△AQG 的面積十△GRI 的面積)
=△ABI 的面積一(△ACG 的而積十△FGI 的面積)
即 JG=
JG= GB,這裡
GB,這裡 JG 表示以J 和G 為頂點的矩形的面積,
JG 表示以J 和G 為頂點的矩形的面積, GB 類似地定義。同理,
GB 類似地定義。同理, KE=
KE= EB,相減可得
EB,相減可得 JG-
JG- KE=
KE= GD,即:(FI-DH)×AC=ED×DF,亦即
GD,即:(FI-DH)×AC=ED×DF,亦即









影差× (日高-表高)=表高×表距。
這就得到了日高公式。
海島公式
日高公式可用來測天,也可藉以量地。比趙爽稍晚的魏晉數學家劉徽就寫了一部叫《海島算經》的著作,套用勾股定理解決各種測量問題,其中第一個問題是測量海島的高度(圖3),劉徽給出了著名的海島公式(顯然,將《周髀算經》中的日高公式改日高為島高,就是海島公式):
島高=(表高×表距)/ 表目距的差+ 表高。
 圖3
圖3