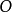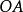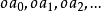基本介紹
- 中文名：斜螺旋面
- 外文名：oblique helicoid
- 所屬學科：數學
- 所屬問題：畫法幾何與工程圖學(曲線曲面)
- 相關概念：螺旋面，三視圖等
總體介紹,斜螺旋面形成,斜螺旋面的投影,
總體介紹
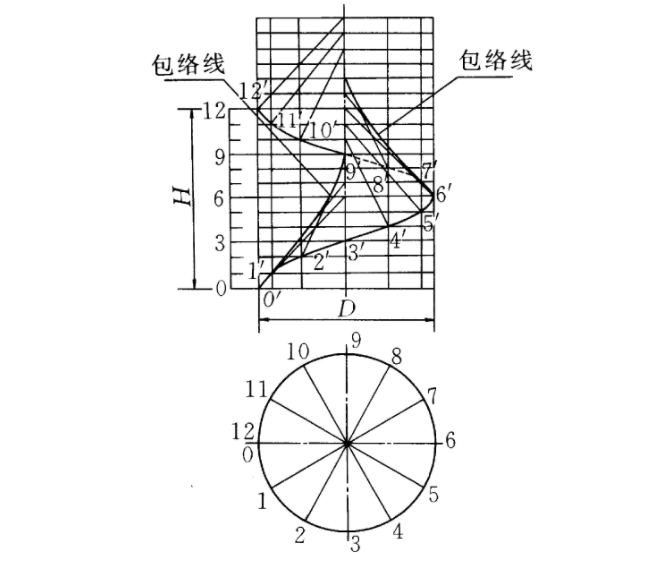
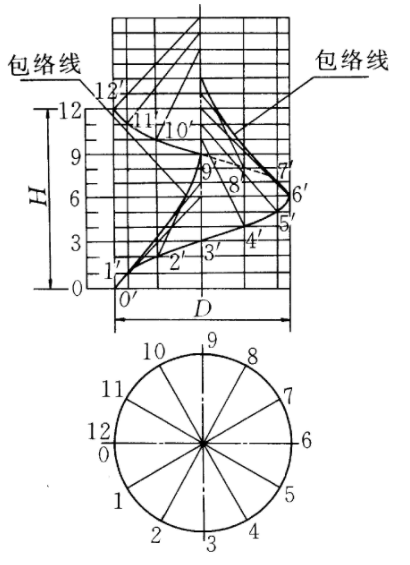
斜螺旋面是一種常見的螺旋面，以任意迴轉面螺旋線為導線，當直母線運動時始終與迴轉面軸線成定角斜交所形成的曲面稱為斜螺旋面。若直母線沿一條圓柱螺旋線運動並始終與其軸線成定角斜交，則形成圓柱斜螺旋面。如下圖所示為一右旋圓柱斜螺旋面，設螺旋線的軸線為鉛垂線，直素線與軸線交成定角，螺旋線導圓柱直徑為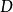
，導程為
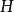，右旋。該螺旋面投影作法是：畫出輔助圓柱面的兩投影；在水平投影上，以
為起點，將圓分成等分，作為斜螺旋面各素線的水平投影；在正面投影上，從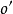
作一直線與軸線成已知直素線與軸的定角，即為斜螺旋面一條素線的正面投影。如此做出一系列素線，判別可見性，再畫出外形輪廓所需的包絡線。
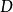
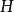
右旋圓柱斜螺旋面斜螺旋面形成
一直母線沿著曲導線為圓柱螺旋線及直導線為圓柱軸線運動，且始終與軸線相交成一定的角度(不等於90°)，即與軸線所垂直的平面成相同傾角
而形成曲面，稱為斜螺旋面。
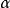
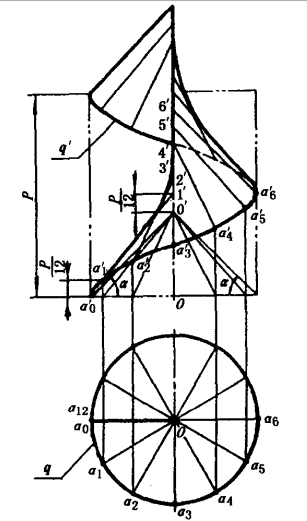圖1(a) 圖1(b)(右側為放大圖) |   |
如圖1(a)所示，直母線為
繞著軸
旋轉形成一圓錐面，圓錐面上一條素線與
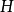面成角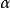
，斜螺旋面的素線必與圓錐面上某一相應素線平行，因此圓錐面稱為斜螺旋面的導錐面。
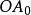
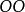
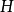
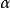
斜螺旋面的投影
在投影圖上表示斜螺旋面，一般只畫曲導線(圓柱螺旋線)、直導線(圓柱軸線)、若干條素線以及決定斜螺旋面投影範圍的外輪廓線。
作圖[圖1(b)]：
(1)先畫出螺旋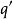線
及圓柱軸線
的投影；
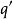
(2)作出導錐兩面投影，在軸線上定出導錐頂點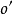
及畫出與軸線夾角
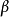(與
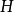面夾角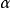
)的導錐輪廓線，得導錐正面投影；
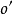
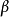
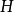
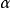
(3)通過錐頂點作出導錐一系列素線(此例為12條)，在底圓等分12等分點，在螺旋線找出對應點，過螺旋線各對應點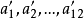
，引與導錐相對應的素線的平行線，交於軸線上
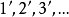，即得斜螺旋面一系列素線的正面投影；
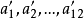
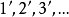
(4)作這些素線投影的包絡線，就是斜螺旋面的外形輪廓線的正面投影。
水平投影的斜螺旋面的外形輪廓線，以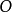
點為圓心，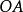
為半徑的圓周，各素線
的水平投影為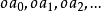
這些線是過圓心的射線。
