斜漸近線是與函式圖像無限接近,但永不相交的一條(或幾條)直線。
基本介紹
- 中文名:斜漸近線
- 外文名:Slant Asymptote
- 套用領域:函式-微積分
- 類別:數學術語
定義,規範求法,求法證明,注意事項,
定義
若當x趨向於無窮時,函式y=f(x)無限接近一條固定直線y=Ax+B(函式y=f(x)與直線y=Ax+B的垂直距離PN無限小,且limPN=0),當然也即PM=f(x)-(Ax+B)的極限為零,則稱y=Ax+B為函式y=f(x)的斜漸近線。
規範求法
分析(在x趨向無窮時)


斜漸近線的正確求法(在x趨向於無窮時)


所以f(x)的斜漸近線方程為
y=Ax+B
求法證明
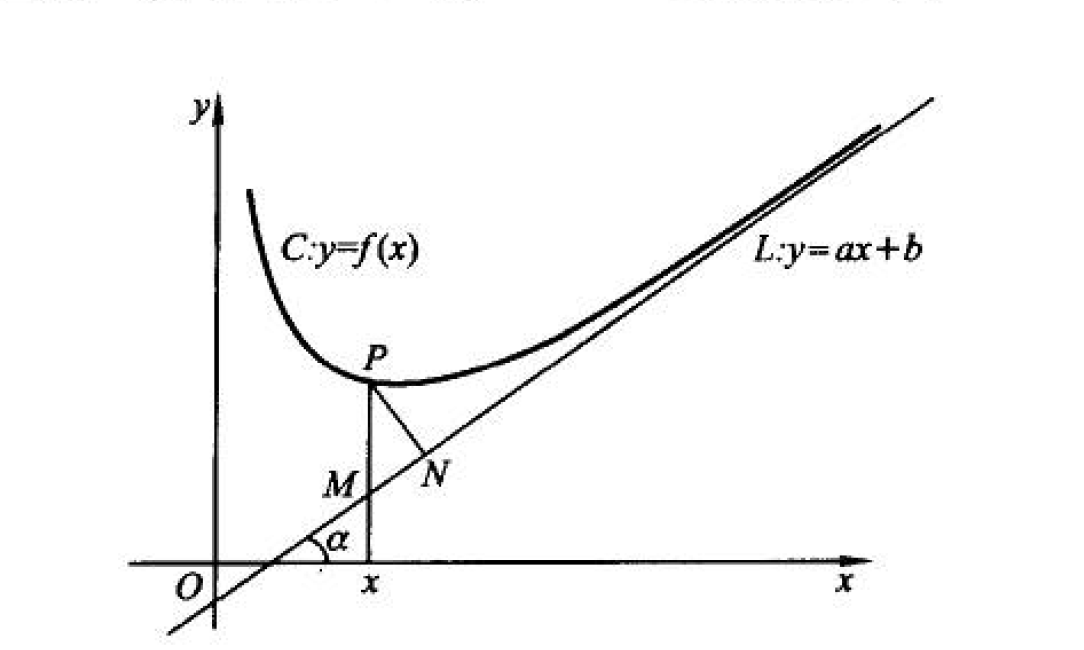 斜漸近線
斜漸近線如圖所示,
直線y=Ax+B與x軸正向夾角為α,則有
PN=PM·cosα=[f(x)-(Ax+B)]cosα .
按照斜漸近線定義,我們知道有limPN=0,而cosα是常數,所以
lim[f(x)-(Ax+B)]=0 .
所以可得:
A=lim[f(x)/x] ,B=lim [f(x)-ax] .
反之,亦然,證畢。
注意事項
當a=0時,有limf(x)=b (x趨向於無窮時),此時稱y=b為函式f(x)的水平漸近線。所以,水平漸近線只是斜漸近線的一種特殊情況。解題時,我們可以不考慮水平漸近線,而只考慮斜漸近線和鉛直漸近線。