斜二測畫法是作空間幾何直觀圖的一種有效方法,是空間幾何直觀圖的畫法基礎。它的口訣是:平行改斜垂依舊,橫等縱半豎不變;眼見為實遮為虛,空間觀感好體現。
在已知圖形中平行於y軸的線段,在直觀圖中畫成平行於y'軸,且長度為原來的二分之一。斜二側畫法的面積是原來圖形面積的√2/4倍。
基本介紹
- 中文名:斜二測畫法
- 外文名:Oblique two method of painting
- 又稱:斜二測法
- 歸屬學科:數學
- 用於:作空間幾何直觀圖
- 面積關係:新圖形面積是原圖形的√2/4倍
- 基本步驟:建系;描點;連線
定義,直觀圖,斜二測畫法,步驟,平面圖形,立體圖形,例題,
定義
直觀圖
所謂直觀圖,是指把空間圖形畫在平面內,使得既富有立體感,又能表達出圖形各主要部分的位置關係和度量關係的圖形。空間幾何體的直觀圖是一種平行投影下的圖像。
斜二測畫法
斜二測畫法是作空間幾何直觀圖的一種有效方法,是空間幾何直觀圖的畫法基礎。在已知圖形中平行於y軸的線段,在直觀圖中畫成平行於y'軸,且長度為原來的二分之一倍。斜二側畫法的面積是原來圖形面積的 倍。
倍。

口訣:平行改斜垂依舊,橫等縱半豎不變;眼見為實遮為虛,空間觀感好體現。
步驟
平面圖形
(1) 建立平面直角坐標系在已知平面圖形中取互相垂直的x軸和y軸,兩軸相交於點O;
(2) 畫出斜坐標系:在畫直觀圖的紙上(平面上)畫出對應的x'軸和y'軸,兩軸相交於點O',且使∠x'O'y' =45°(或135°),它們確定的平面表示水平平面;
(3) 畫對應圖形:在已知圖形平行於x軸的線段,在直觀圖中畫成平行於x'軸,長度保持不變;在已知圖形平行於y軸的線段,在直觀圖中畫成平行於y'軸,且長度為原來的一半;
(4)對於一般線段,要在原來的圖形中從線段的各個端點引垂線,再按上述要求畫出這些線段,確定端點,從而畫出線段;
(5) 擦去輔助線:圖畫好後,要擦去x'軸、y'軸及為畫圖添加的輔助線;
例如:如圖1,用斜二測畫法畫出水平放置的正六邊形的直觀圖。
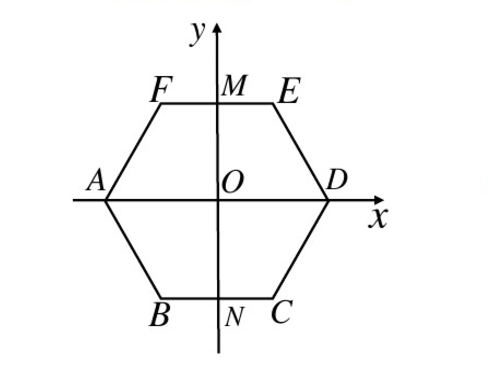 圖1 六邊形
圖1 六邊形解:
第一步:在六邊形ABCDEF中,取AD所在直線為x軸,對稱軸MN所在直線為y軸,兩軸交於O。畫出相應的x'軸和y'軸,兩軸交於O',使∠x'O'y' =45°。
 圖2 畫出坐標軸
圖2 畫出坐標軸第二步:以O'為中心,在x'軸上取A'D'=AD,在y'軸上取M'N'=1/2MN。以點N'為中心,畫B'C'平行於x‘軸,並且等於BC。再以M'為中心,畫E'F'平行於x'軸,且等於EF。
 圖3
圖3第三步:連線A'B',A'F',A'D',C'D',並擦去輔助線x'軸、y'軸,便可獲得正六邊形ABCDEF水平放置的直觀圖A'B'C'D'E'F'。
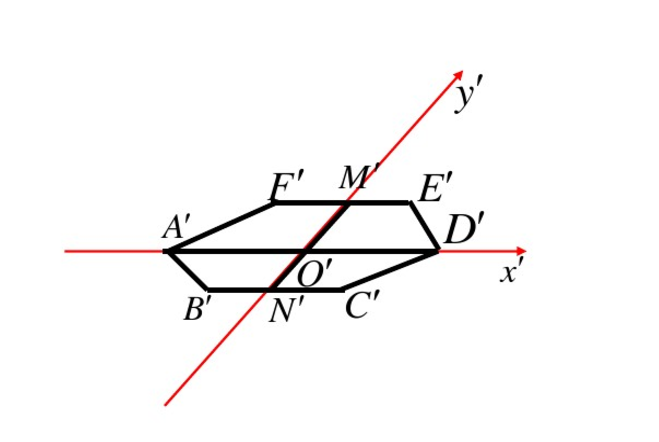 圖4
圖4立體圖形
利用斜二測畫法作幾何體直觀圖的一般步驟如下:
(1)畫軸:畫x.y.z三軸交原點,使xOy=45°、xOz=90°;
(2)畫底面:在相應軸上取底面的邊,並交於底面各頂點;
(3)畫側棱或橫截面側邊,使其平行於z軸;
(4)成圖:連線相應端點,去掉輔助線,將被遮擋部分改為虛線等。
畫幾何體的直觀圖時,如果不作嚴格要求,圖形尺寸可以適當選取。用斜二測畫法畫圖的角度也可是自定,但要求圖形有一定的立體感,作水平放置的圓的直觀圖可藉助橢圓模板。
例題
一個水平放置的平面圖形的斜二測直觀圖是一個底角為45°、腰和上底長均為1的等腰梯形,求該平面圖形的面積?
方法1:
等腰梯形的高為: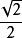 ,上底是1,下底是
,上底是1,下底是 ,面積為:
,面積為:
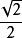


因為斜二側畫法的面積是原來圖形面積的 倍,故原來圖形面積為:
倍,故原來圖形面積為: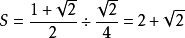

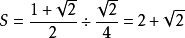
方法2:
由於它左邊的底角是45°,所以可知平面圖是個直角梯形,可以求出上底是1,下底是

斜二測畫法是保持平行於x軸的線段長度不變,平行於y軸的線段變為原來的一半,所以可知直角梯形的高是2
所以


