基本介紹
- 中文名:數乘變換
- 外文名:Number multiplication transformation
- 所屬學科:數學
- 所屬問題:線性代數(向量空間)
- 簡介:一種線性變換
基本介紹
線性變換的概念











數乘變換的概念


相關性質























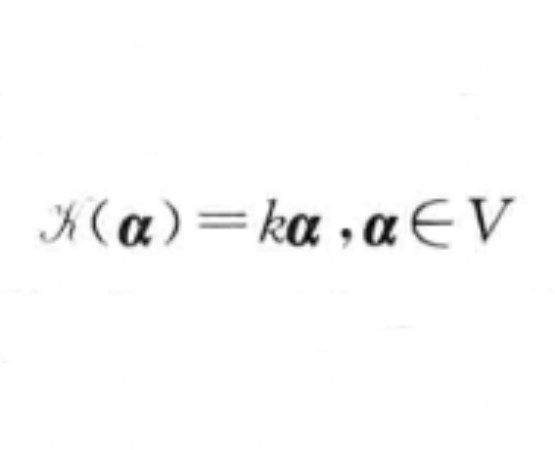




































數乘變換(Number multiplication transformation)是一種線性變換,設V是數域P上的一個線性空間,k是P中的一個數,對任意α∈V,由σ(α)=kα所決定的線性變換σ,稱為數乘變換,記為k*...
,則右乘變換 ,它把 映成乘積 ,就是集合G 上的一個變換。當 g 取遍 G 中所有的元素時,全體右乘變換 在變換的乘法下成為一個 。它是集合G 上的變換群,而映射 是群G 到變換群 的同構。 [1] ...
定義:如果B可以由A經過一系列初等變換得到,則稱矩陣A與B稱為等價 初等行變換 定義:所謂數域P上矩陣的初等行變換是指下列3種變換:1)以P中一個非零的數乘矩陣的某一行 2)把矩陣的某一行的c倍加到另一行,這裡c是P中的任意...
我們可以看到這樣的旋轉變換的目的就是把坐標系旋轉後來看一下。這樣的旋轉角度一旦確定以後,我們就能夠得到原來的老坐標下的坐標點在新坐標系下的坐標為 。注意的是,這裡的坐標是右乘變換矩陣。線性變換數學定義在一般的高等代數學書...
用 f(t)表示實變數t的一個函式,F(s)表示它的拉普拉斯變換,它是復變數s=σ+jω;的一個函式,其中σ和ω; 均為實變數,j²=-1。F(s)和f(t)間的關係由下面定義的積分所確定:如果對於實部σ >σ的所有s值上述積分均...
這裡主要是線性變換,線性變換針對於實際對象主要完成類似於旋轉和尺度變換方面的操作,而這種操作也牽涉到表達的問題。為了保持與空間的一致性,我們也同樣是在在特定的基下來表示,從而線性變換就具體化為一個變換矩陣,並且,在不同的基...
我們可以看到這樣的旋轉變換的目的就是把坐標系旋轉後來看一下。這樣的旋轉角度一旦確定以後,我們就能夠得到原來的老坐標下的坐標點在新坐標系下的坐標為 。注意的是,這裡的坐標是右乘變換矩陣。線性代換數學定義在一般的高等代數學書...
基本變換 正交矩陣的最基本置換是換位(transposition),通過交換單位矩陣的兩行得到。任何n×n置換矩陣都可以構造為最多n−1次換位的積。構造自非零向量v的Householder反射,這裡的分子是對稱矩陣,而分母是v的平方量的一個數。這是...
證明 我們只需證明行列式因子在任意一種初等變換下不變就可以了,對第一種初等變換,交換λ一矩陣 的任兩行,顯然 A (λ )的i階子式最多改變一個符號,因此行列式因子不改變。對第二種初等變換,A (λ )的i階子式與變換後矩陣...
在泛函分析中,卷積、旋積或褶積(英語:Convolution)是通過兩個函式f和g生成第三個函式的一種數學運算,其本質是一種特殊的積分變換,表征函式f與g經過翻轉和平移的重疊部分函式值乘積對重疊長度的積分。如果將參加卷積的一個函式看作...
與積分相似:連續(或非連續可積)函式的連續和為積分,連續相乘即為積乘。積分表示從一個維度到高一級的維度的轉換,而積乘表示維度的連續變換。定義 與積分相似:連續(或非連續可積)函式的連續和為積分,連續相乘即為積乘。表示函式...
