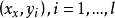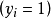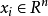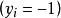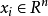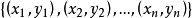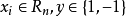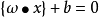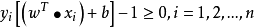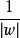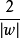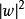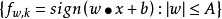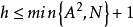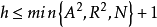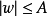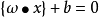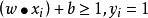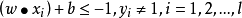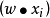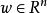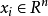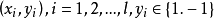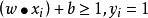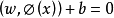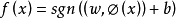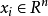支持向量機是針對二值分類問題提出的，並且成功地套用子解函式回歸及一類分類問題。雖然支持向量機在解決二值分類問題時獲得了巨大的成功，但實際套用中的大量多值分類問題也進一步要求如何將支持向量機推廣到多分類問題上。
基本介紹
- 中文名：支持向量機分類
- 外文名： Support Vector Machine classification
簡介,支持向量機分類,線性可分,線性不可分,
簡介
支持向量機是針對二值分類問題提出的，並且成功地套用子解函式回歸及一類分類問題·雖然支持向量機在解決二值分類問題時獲得了巨大的成功，但實際套用中的大量多值分類問題也進一步要求如何將支持向量機推廣到多分類問題上，目前有以下幾種常用的方法：
- 一對多法。其思想是把某一種類別的樣本當作一個類別，剩餘其他類別的樣本當作另一個類別，這樣就變成了一個兩分類問題。然後，在剩餘的樣本中重複上面的步驟`這種方法箱要構造k個svM模型，其中，k是待分類的個數。這種方案的缺點是訓練樣本數目大，訓練困難。
- 一對一方法。其做法是在多值分類中，每次只考慮兩類樣本，即對每兩類樣本設計一個SVM模型，因此，總共需要設計k(k一l)2/個SVM模型.這種做法需要構造多個二值分類器，並且測試時需要對每兩類都進行比較，導致算法計算複雜度很高。
- SVM決策樹法。它通常和二叉決策樹結合起來，構成多類別的識別器。這種方法的缺點是如果在某個節點上發生了分類錯誤，將會把錯誤延續下去，該節點後續下一級節點上的分類就失去了意義。weston雖然提出了用一個最佳化式解多值分類問題’〕，但由於其變數t數目過多，所以只能在小型問題的求解中使用。一類分類方法的出現為異常值檢測提供了一條新的思路，該方法通過核映射思想確定一個包含正類樣本的緊緻區域，以便使異常值更容易暴露出來，從而達到檢測的目的。
支持向量機分類
在統計學習理論中，我們經常使用的就是支持向量機分類，因為它的效果非常好，其中心思想是把結構風險最小化原則套用於分類領域中。
如何從訓練樣本中找到一個支持向量，能夠建構出最好的分類超平面，這是支持向量機的核心內容，它是從線性可分情況下的最優分類超平面發展而來的。用數學語言描述就是求解一個二次規劃問題，這一問題的約束條件可以用不等式的形式表述出來。
我們將訓練樣本集
分成兩個類別，標記為正
的屬於第一類
；標記為負
的屬於第二類 。如果我們建構的決策函式能夠將被測試數據分開，那么學習目標就達成了。現將訓練樣本集分為兩種情況進行討論，一種為線性的，另一種為非線性情況。
設訓練樣本集為
其中
不妨假設存在一個超平面能夠線性劃分這個樣本集。設這個超平面為
如果存在一個超平面能夠將訓練樣本集中的所有向量都正確劃分，而且能達到最大邊緣化，那這個超平面叫做最優超平面。支持向量就是距離超平面最近的訓練樣本集中的向量，支持向量和超平面之間是一一對應的關係。
首先考慮線性可分的情況，假定支持向量滿足條件：
因為超平面和支持向量之間的距離是
，可知兩個支持向量間的距離是
。所以只要求出
的最小值，就能構造出最優超平面。當樣本點在超球體內部時，
如果超球體的半徑是R，那么上式就細化為
支持向量空間的維數用N表示，R是超球體半徑，這個超球體能夠覆蓋所有的支持向量，
.由此可知，VC維隨w的減小而減小，所以支持向量機方法的目的是找到最小的w，從而解決風險最小化問題。
線性可分
如果存在分類超平面
使得：
那么這個訓練集就是線性可分的，其中
表示向量
與 的內積。
假設在三維空間中，存線上性可分的兩個類別的訓練樣本集
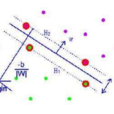
其中樣本維數n=3，樣本類別+1或-1用iy來表示.我們致力於找到一個能夠準確的把兩類樣本區分開的分類平面H，並且他們之間的分類間隔是最大的，那么這個分類平面H就被叫做最優分類超平面。
分類平面H、分類平面1H和分類平面2H將幾何空間分成三個分類平面，它們之間是平行的位置關係，分類平面H處於分類平面1H和分類平面2H的中間，並且他們之間的距離都是相等的，我們用D來表示。如果樣本點得類別為+1，那么它就落在分類平面1H上，如果樣本點得類別為-1，那么它就落在分類平面1H上。從數學上看，分類平面H的方程為
其中w，x表示的是向量之間的內積，權值用w表示，常數為b。
線性不可分
最初研究的支持向量機問題都是線性可分的，但在實際套用中多數為線性不可分的情況，為了解決這一難題，我們將輸入的數據通過非線性變換(x)將其映射到高維特徵空間中去。在高維特徵空間中，原空間輸入的非線性分類就轉化為線性問題。在無限大的高維特徵空間中，我們通過構建最優分類超平面：
得到決策函式為
通過式子可以發現，不同於其他最優分類超平面需要以多種形式來描述特徵空間，我們所構建的超平面只需要計算向量的內積。假定，把輸入向量映射到無限高維特徵空間，即由Hilbert-Schmidt理論可知，高維特徵空間中的內積可以表示為,我們稱K(x1,x2)為核函式，它是滿足Mercer定理的對稱函式。。核函式相對映射函式簡單，而且映射函式的維數很高，因此，引入核函式才能解決維數太大的難題。
