擺線齒輪是齒廓為各種擺線或其等距曲線的圓柱齒輪的統稱。擺線齒輪的齒數可很少,常用在儀器儀表中,較少用作動力傳動,其派生型式擺線針輪傳動則套用較多。
基本介紹
- 中文名:擺線齒輪
- 外文名:Cycloidal gear
- 類型:圓柱齒輪
- 特點:傳動平穩
- 學科:機械原理
- 套用領域:機械傳動
擺線齒輪齒廓
 擺線齒廓的形成
擺線齒廓的形成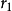


符合嚙合基本定律
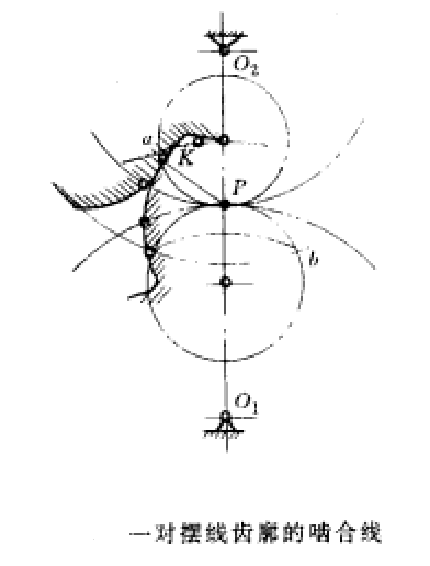 一對擺線齒廓的嚙合線
一對擺線齒廓的嚙合線
擺線齒輪特點

擺線齒輪套用



 羅茨齒輪
羅茨齒輪
擺線齒輪是齒廓為各種擺線或其等距曲線的圓柱齒輪的統稱。擺線齒輪的齒數可很少,常用在儀器儀表中,較少用作動力傳動,其派生型式擺線針輪傳動則套用較多。
 擺線齒廓的形成
擺線齒廓的形成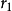


 一對擺線齒廓的嚙合線
一對擺線齒廓的嚙合線




 羅茨齒輪
羅茨齒輪擺線齒輪是齒廓為各種擺線或其等距曲線的圓柱齒輪的統稱。擺線齒輪的齒數可很少,常用在儀器儀表中,較少用作動力傳動,其派生型式擺線針輪傳動則套用較多。...
由一對擺線齒輪組成的齒輪傳動。擺線齒輪的齒廓由內擺線或外擺線組成 (圖中)。滾圓S 在節圓OJ1外面滾動形成齒頂曲線bc,在節圓OJ2內面滾動形成齒根曲線aa′;...
圓錐延伸外擺線齒輪又稱奧里康制螺旋圓錐齒輪。是指輪齒的齒面與分度圓錐面的交線(即齒線)為延伸外擺線一段的曲齒圓錐齒輪。...
中文名稱 擺線[圓柱]齒輪 英文名稱 cycloidal [cylindrical] gear 定義 齒廓為擺線形狀的圓柱齒輪。 套用學科 機械工程(一級學科),傳動(二級學科),齒輪傳動(...
擺線針輪傳動是指由外齒輪齒廓為變態擺線、內齒輪輪齒為圓銷的一對內嚙合齒輪和輸出機構所組成的行星齒輪傳動。...
擺線圓柱齒輪編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:2次歷史...
擺線內嚙合齒輪泵,又稱擺線轉子泵,是由小齒輪(內轉子)和內齒輪(外轉子)組成。兩個齒輪均為擺線齒輪,小齒輪比內齒輪只少一個齒。由於內外轉子是多齒嚙合,這就...
擺線齒輪測量儀將雷射束投射到測頭的反射鏡上,就能精確地測量齒形等各項誤差參數,並能自動演算誤差量。...
擺線針輪減速機,是一種套用行星式傳動原理,採用擺線針齒嚙合的新穎傳動裝置。擺線針輪減速機全部傳動裝置可分為三部分:輸入部分、減速部分、輸出部分。...
擺線齒輪泵也是利用齒間密封容積的變化來實現吸油壓油的。它是由配油盤(前、後蓋)、外轉子(從動輪)和偏心安置在泵體內的內轉子(主動輪)等組成。...
擺線少齒差傳動指由擺線少齒差齒輪副、偏心元件及輸出機構組成的傳動機構。...... 擺線少齒差傳動指由擺線少齒差齒輪副、偏心元件及輸出機構組成的傳動機構。...
定義 由齒數差很少的擺線齒輪和針輪組成的齒輪副。 套用學科 機械工程(一級學科),傳動(二級學科),齒輪傳動(三級學科) 以上內容由全國科學技術名詞審定委員會審定...
內嚙合擺線齒輪泵,它是由配油盤(前、後蓋)、外轉子(從動輪)和偏心安置在泵體內的內轉子(主動輪)等組成。內、外轉子相差一齒,圖中內轉子為六齒,外轉子為七...
擺線針輪減速機是一種套用行星式傳動原理,採用擺線針齒嚙合的新穎傳動裝置。擺線針輪減速機全部傳動裝置可分為三部分:輸入部分、減速部分、輸出部分。在輸入軸上裝...
19世紀50年代末期,最初的低速大扭矩液壓馬達是由油泵的一個定轉子部件發展而來的,這個部件由一個內齒圈和一個與之相配的齒輪或轉子組成。...
錐齒輪加工刀具是專用於切削各種錐齒輪齒形的齒輪加工刀具。 ...... 定義 在奧列康工具機上加工延伸外擺線齒錐齒輪的銑刀。 套用學科 機械工程(一級學科),刀具(二...
圓弧齒輪傳動齒廓為圓弧形的點嚙合齒輪傳動。通常有兩種嚙合形式:小齒輪為凸圓弧齒廓,大齒輪為凹圓弧齒廓,稱單圓弧齒輪傳動。圓弧齒輪是指齒廓為圓弧形的點嚙合...
擺線轉子馬達是指齒廓線為擺線的特殊內噬合齒輪式液壓馬達定子為內齒輪,轉子為外齒輪。...
BMF系列擺線液壓馬達是一種內嚙合擺線齒輪式的小型、低速、大扭矩液壓馬達。它的結構簡單,外觀新穎,低速第速穩定性好使用壽命長,是取代進口馬達的首推產品。...
行星擺線減速機是一種套用行星傳動原理,採用擺線針輪嚙合,設計先進、結構新穎的減速機構。這種減速機在絕大多數情況下已替代兩級、三級普通圓柱齒輪減速機及圓柱蝸桿...
18世紀,歐洲工業革命以後,齒輪傳動的套用日益廣泛;先是發展擺線齒輪,而後是漸開線齒輪,一直到20世紀初,漸開線齒輪已在套用中占了優勢。...
