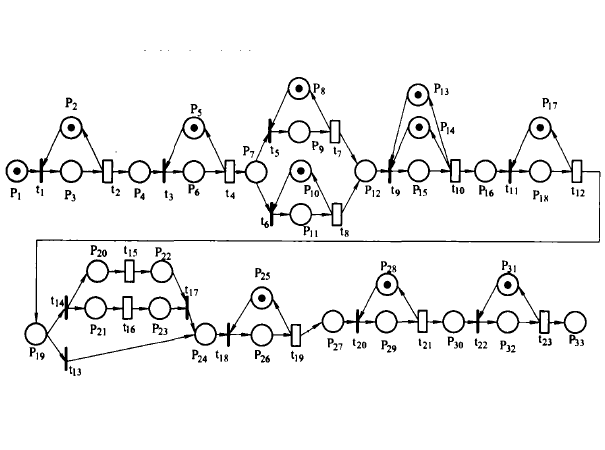
基本介紹
- 中文名:擴展隨機佩特里網
- 外文名:Extend stochastic Petri nets
- 別稱:擴展隨機Petri網
- 簡稱:ESPN
- 領域:計算機
- 特點:允許存在任意分布的時間變遷
簡介,ESPN的定義,定義,點火規則,ESPN性能分析,矩母函式與傳遞函式,基於行為表達式的分析方法,ESPN模型的分析方法及步驟,
簡介
Petri網是一種描述離散系統的建模工具,尤其適合於順序、並發、衝突和同步過程的分析。因此,基於Petri網的製造系統建模及分析技術被廣泛的提出。各種不同類型的Petri網(如面向對象Petri網、著色Petri網、隨機Petri網以及變結構Petri網等)分別適用於不同類型的製造系統。
為了對離散事件動態系統性能進行分析,引入了時間petri網(TPN)。在TPN中系統固定時延與庫所或變遷聯繫在一起,除了能分析系統結構外,還能分析系統的循環周期性能(如系統吞吐率、資源利用率等)。然而,由於大量隨機現象的存在,確定時間的Petri網對真實系統的模擬還不充分。隨機petri網(SPN)及廣義隨機Petri網(GSNP)的出現提高了對真實系統的模擬程度,其計算結果更加精確,其中GSPN因減少了SPN狀態空間而得到更廣泛套用。但是,真實的製造系統是個複雜過,其中既包括了確定時間的變數也包括了隨機時間變數,擴展隨機petri網(EPSN)的提出進一步提高了對製造系統的建模及分析能力。ESPN中可包含任意分布的變數。
ESPN的定義
ESPN的特點是時間變遷對應一個任意分布的隨機變數。
定義
定義1:ESPN是一個七元組N = (P,T,I,O,H,m,F),其中,
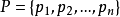
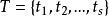
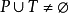
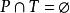
I: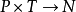 ,是一個輸入函式,其中N={0,1, 2,…};
,是一個輸入函式,其中N={0,1, 2,…};
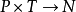
O: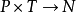 ,是一個輸出函式;
,是一個輸出函式;
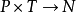
H: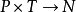 ,是一個抑制函式;
,是一個抑制函式;
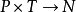
m: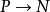 ,是一個標識,標識中的第i分量是第i個Place的Token數。其初始標識記為
,是一個標識,標識中的第i分量是第i個Place的Token數。其初始標識記為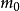 ;
;
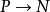
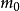
F: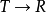 ,是一個矢量,矢量的分量對應擴展分布的點火時延。
,是一個矢量,矢量的分量對應擴展分布的點火時延。
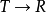
點火規則
(1)在標識m中,變遷 被使能,若且唯若:
被使能,若且唯若: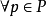 ,
,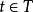 ,
, 並且如果
並且如果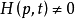 ,m(p)<H(p,t)。
,m(p)<H(p,t)。

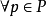
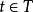

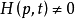
(2)若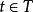 在標記m下被使能,按照如下激活規則產生新標記
在標記m下被使能,按照如下激活規則產生新標記 ,
,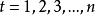 。
。

ESPN性能分析
製造系統Petri網模型的行為表達式反應了製造系統的產品加工過程。根據行為表達式可以求得Petri網的傳遞函式,從而可以利用矩母函式思想,實現對擴展隨機Petri網的性能分析。在說明ESPN性能分析方法和步驟之前,先引入矩母函式與傳遞函式以及基於行為表達式分析方法的概念。
矩母函式與傳遞函式
定義2:設x是一個隨機變數,則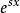 的期望值稱為x的矩母函式,記為
的期望值稱為x的矩母函式,記為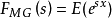 (x為實變數)。
(x為實變數)。
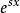
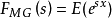
若x為離散變數,具有機率分布函式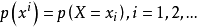 ,則矩母函式為:
,則矩母函式為: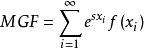 。
。
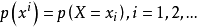
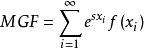
若x為連續隨機變數,且機率密度函式為f(x),則x的矩母函式為: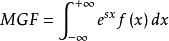 。
。
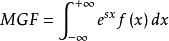
定義3:在一個任意分布的隨機Petri網中,對於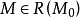 ,
,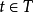 ,令
,令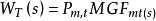 ,則
,則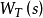 為t在M下的傳遞函式。其中
為t在M下的傳遞函式。其中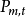 為M下t被引發的機率,
為M下t被引發的機率,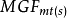 為M下t的矩母函式。
為M下t的矩母函式。
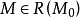
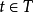
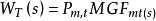
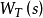
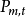
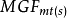
基於行為表達式的分析方法
一個行為表達式或者是一個複合式,或者是一個冪級式。它可以描述有界Petri網,或者某些無界Petri網(表達式存在的Petri網)。根據表達式並藉助下面幾個定理,可以求得Petri網的傳遞函式W,再利用矩母函式的相關分析方法便可對任意分布的隨機Petri網進行品質分析。
定理1:設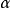 是一個單項式,
是一個單項式,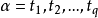 ,則
,則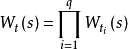 。
。
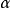
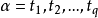
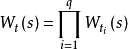
定理2:設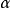 是一個標準多項式
是一個標準多項式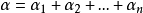 ,則
,則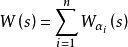 。
。
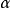
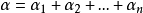
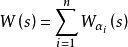
定理3:設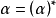 ,則
,則 。
。
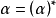

ESPN模型的分析方法及步驟
基於行為表達式的分析方法一般為:建立系統的Petri網模型、給出系統的行為表達式、計算行為表達式的傳遞函式以及採用矩母函式相關方法進行性能指標的計算。具體步驟如下。
(1) 建立ESPN模型。給出相應不同加工設備的ESPN模組。
(2) 構造系統行為表達式。產生系統的行為表達式,並將多項式化為標準多項式形式。
(3) 求傳遞函式。根據所給的分布參數以及行為表達式結構,求出各事件的引發機率及其矩母函式,再根據傳遞函式定義得到各事件的傳遞函式。
(4) 重新標號行為表達式。根據第三步的計算結果,為行為表達式重新標號,以區別表示式中具有不同傳遞函式的同一事件。
(5) 重新計算傳遞函式。根據上述定理1~3計算標號後的行為表達式的傳遞函式。
(6) 計算系統性能。基於前面的結果和矩母函式的有關方法進行各性能指標的計算,從而獲得系統的定量分析結果。