基本概述
在載荷作用下,梁橫截面上一般同時存在
剪力和
彎矩。由
切應力τ構成剪力,由
正應力σ構成彎矩,如圖1所示。由正應力與切應力引起的彎曲分別稱為彎曲正應力與彎曲切應力。
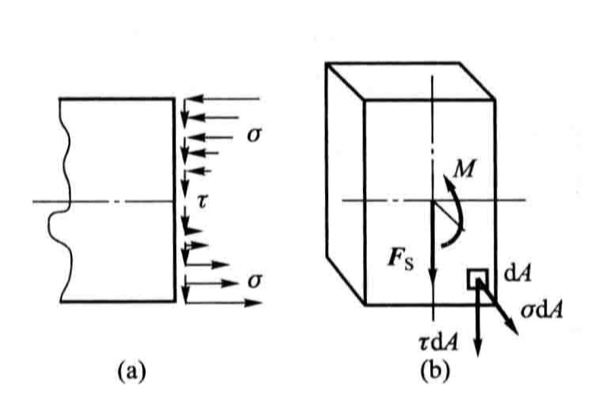 圖1
圖1彎曲正應力的一般公式
推導純彎曲梁橫截面的正應力公式,與推導扭轉切應力公式相似,也需要從變形兒何關係、物理關係和靜力學三方面來考慮。
變形幾何關係
純彎曲時梁的縱向“纖維”由直線變為圓弧,相距
的兩橫截面1'-1'和2'-2'繞中性軸發生相對轉動,如圖2所示。橫截面1'-1'和2'-2'延長相交於O點,O點即為中性層的曲率中心。設中性層的曲率半徑為ρ,此兩橫截面夾角為
,則距中性層為y處縱向“纖維”ab的正應變為
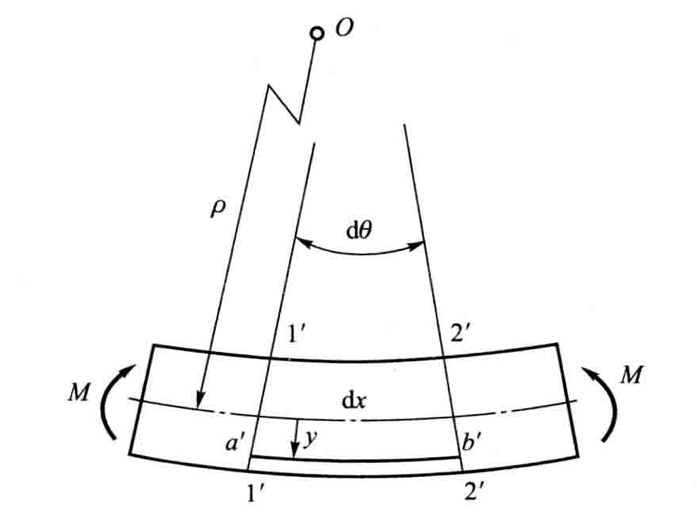 圖2
圖2實際上,由於距中性層等遠各縱向“纖維”的變形相同,所以,上述正應變ε即代表距中性層為y的任一縱向“纖維”的正應變。
物理關係
根據單向受力假設,各縱向”纖維”處於單向拉仲或壓縮狀態,因此,當正應力不超過材料的比例極限時,胡克定律成立,由此得橫截面上距中性層y處的正應力為
該式就是梁純彎曲時橫截面上的正應力分布規律。由此式可知,橫截面上任一點處的正應力與該點到中性軸的距離成正比,距中性軸等遠的同一橫線上的各點處的正應力相等,中性軸各點處的正應力均為零。
靜力學關係
上面雖已得到正應力分布規律,但還不能用所給公式直接計算梁純彎曲時橫截面上的正應力。至此有兩個問題尚未解決:一是中性層的曲率半徑ρ仍未知;二是中性軸位置未知,故式中之y還無從確定。解決這兩個問題,需要藉助於靜力學關係。
 圖3
圖3令橫截面縱向對稱軸為y軸,中性軸為x軸,梁軸線為x軸,在坐標(y,a)處取一微面積dA,法向微內力為ρdA(圖3),橫截面各微面積上的法向微內力ρdA組成一空間平行力系,而且橫截面上不存在軸力,僅存在位於x-y平面內的彎矩M,因此
得:
式中左邊的積分代表橫截面對z軸的靜矩
。只有當z軸通過橫截面形心時,靜矩
才為零。由此可見,中性軸通過橫截面形心。
可得:
此式為用曲率表示的彎曲變形公式。公式中
代表橫截面對z軸的慣性矩。
由推出的公式易得純彎曲時梁橫截面上的正應力計算公式為:
此式為彎曲正應力的一般公式。
彎曲正應力公式的套用范
彎曲正應力公式是在純彎曲情況下推導的。當梁受到橫向力作用時,在橫截面上,一般既有彎矩又有剪力,這種彎曲稱為橫力彎曲。由於剪力的存在,在橫截面上將存在切應力τ,從而存在切應變γ=τ/G。由於切應力沿梁截面高度變化,故切應變γ沿梁截面高度也是非均勻的。因此,橫力彎曲時,變形後的梁截面不再保持平面而發生翹曲,如圖4中的1-1截面變形後成為1'-1'截面。既然如此,以平面假設為基礎推導的彎曲正應力公式,在橫力彎曲時就不能適用。但是,如果兩截面間沒有載荷作用時,則兩截面的剪力相同,其翹曲程度也相同,由彎矩所引起的縱向纖維的線應變將不受剪力的影響,所以彎曲正應力公式仍然適用。當梁承受分布載荷作用時,兩截面上的剪力不同,因而翹曲程度也不相同,而且,此時縱向纖維還受到分布載荷的擠壓或拉伸作用,但精確分析表明,如果梁長l與梁高h相比足夠大時,這種翹曲對彎曲正應力的影響很小,套用公式計算彎曲正應力仍然是相當精確的。
綜上所述,對於各橫截面剪力相同的梁和各橫截面剪力不相同的細長梁,在純彎曲情況下推導的彎曲正應力公式仍然適用。
 圖1
圖1


 圖2
圖2
 圖3
圖3










