摩萊三角形

在已知△ABC三內角的三等分線中，分別與BC,CA,AB相鄰的每兩線相交於點D，E，F，則三角形DFE是正三角形，這個正三角形稱為摩萊三角形。·

基本介紹

• 中文名：摩萊三角形
• 證明：AE CE交E
• 證明2：BD CD交D
• 證明3：而nsin(α+β)=csinβ

證明過程

AE CE交E

BD CD交D

AF BF交F 記A=3α，B=3β，C=3γ，AE=m，AF=n，△ABC的三邊長為a、b、c．

由於3α+3β+3γ=180°．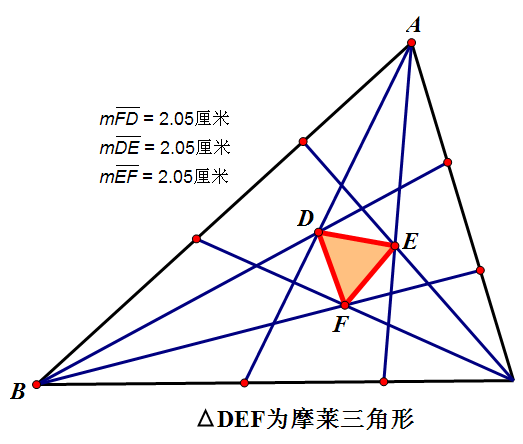

所以α+β+γ=60°．α+β=60°-γ

而nsin(α+β)=csinβ

所以n=csinβ/sin(α+β)=csinβ/sin(60-γ)

類似地m=bsinγ/sin(60-β)

在△ABC中有bsin3γ=csin3β，

從而

m/n

=(sin3β*sinγ*sin(60-γ))/(sin3γ*sinβ*sin(60-β))

=(sin(60+β))/(sin(60+γ))

由於α+β+γ=60°．

所以存在以60°+β，60°+γ和α為內角的三角形，

夾α角的兩邊之比為 (sin(60+β))/(sin(60+γ))=m/n

△EAF與這三角形相似，

從而 ∠AFE=60°+β ∠AEF=60°+γ

同法可證∠BFD=60°+α，

而 ∠AFB=180°-(α+β)

因此 ∠EFA+∠AFB+∠BFD=(60°+β)+(180°-α-β)+(60°+α)=300°

所以∠DFE=60°．

結論

類似地，△DEF的另兩個內角也為60°． 因此△DEF是等邊三角形．