振盪環節(oscillation element)控制系統的一類典型環節。
基本介紹
- 中文名：振盪環節
- 外文名：oscillation element
基本特徵,微分方程,傳遞函式,參數,單位階躍回響,其他,
基本特徵
微分方程
振盪環節的微分方程為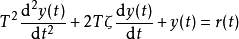
。
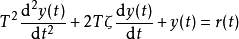
傳遞函式
振盪環節的傳遞函式為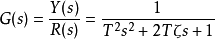
，也可以寫成另外一種形式
。
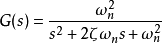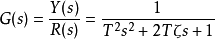
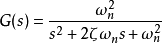
參數
單位階躍回響
在單位階躍作用下，振盪環節輸出量拉普拉斯變換為
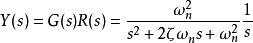
再進行拉普拉斯反變換得到輸出量表達式為
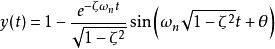
式中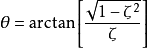
。
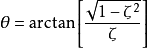
其他
振盪環節的輸入量發生變化時，輸出量常會呈現周期性變化，其頻率僅與環節有關，與信號的幅值和變化速度無關。振盪環節對應於二階常微分方程，它具有振盪特徵的充分必要條件是}<1，即傳遞函式的分母多項式有虛根或共扼複數根.當}<0時，振盪環節出現持續以至發散的振盪，系統為不穩定.當1>參>0時，振盪環節相應於衰減性振盪，系統可穩定工作，但一般希望對它的振盪頻率、幅值和衰減速度進行限制，以免造成不良的後果.
