基本介紹
- 中文名:拓撲生成序列
- 外文名:topogenicsequences
- 化學本質:多肽/蛋白質
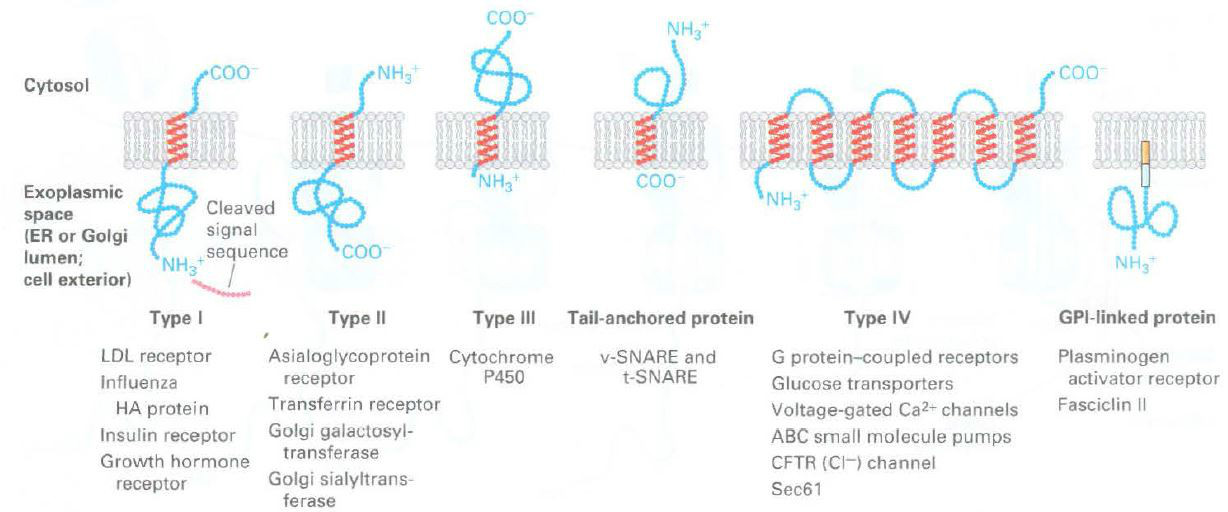
類別 | 類型I | 類型II | 類型III | 類型IV |
跨膜次數 | 1 | 1 | 1 | 大於1 |
N端方向 | 內質網腔(由於細胞膜的保守性也成外質膜面) | 胞質面 | 外質膜面 | 不確定(視基數次跨膜,偶數次跨膜而定) |
是否包含可切除的內質網信號序列 | 是 | 否 | 否 | 否 |


類別 | 類型I | 類型II | 類型III | 類型IV |
跨膜次數 | 1 | 1 | 1 | 大於1 |
N端方向 | 內質網腔(由於細胞膜的保守性也成外質膜面) | 胞質面 | 外質膜面 | 不確定(視基數次跨膜,偶數次跨膜而定) |
是否包含可切除的內質網信號序列 | 是 | 否 | 否 | 否 |
拓撲生成序列(topogenic sequences)為一種特殊的定位多肽鏈,指導內質網跨膜蛋白的生成過程,包括如何插入以及插入方向。拓撲生成序列(topogenicsequences)為一種特殊的定位多肽鏈,指導內質網...
對一個有向無環圖(Directed Acyclic Graph簡稱DAG)G進行拓撲排序,是將G中所有頂點排成一個線性序列,使得圖中任意一對頂點u和v,若邊∈E(G),則u線上性序列中出現在v之前。通常,這樣的線性序列稱為滿足拓撲次序(Topological Order...
拓撲序列是頂點活動網中將活動按發生的先後次序進行的一種排列。 拓撲排序,是對一個有向無環圖(Directed Acyclic Graph簡稱DAG)G進行拓撲排序,是將G中所有頂點排成一個線性序列,使得圖中任意一對頂點u和v,若邊(u,v)∈E(G),...
拓撲空間是一般拓撲學的基本研究對象。確定了拓撲T的集合X稱為拓撲空間,記為(X,T)。具有拓撲結構的抽象空間是弗雷歇(Fréchet,M.-R.)於1906年和里斯(Riesz,F.(F.))於1907年首先引進的。弗雷歇用收斂序列,里斯用聚點分別定義了...
緊拓撲空間上的下半連續函式或序列緊拓撲空間上的依序列下半連續函式可達到其下確界。凸錐 凸錐是一類特殊的凸集。實線性空間中既是凸集又是錐的集合稱為凸錐。凸錐C滿足C+C⊂C。對於X中的任何子集A,由它生成的凸錐是其元素的...
線性圖是一種能推廣圖的許多幾何性質的拓撲空間。泛函分析中的許多運算元集合可以獲得一種特殊的拓撲,在這種拓撲空間中某一類函式序列收斂。有限補拓撲。設X是一個集合。X的所有有限子集的補集加上空集,構成X上的一個拓撲。相應的拓撲...
若是一個訊息是針對計算機中途向下行時,每個系統彈起其沿線於序列中,直到該到達目的地為止。運作 任何特定的菊花鏈形成的兩個網路拓撲結構之一:線性拓撲結構:線性拓撲結構使一台計算機與下一個之間的雙向連結。然而,這是昂貴的計算機...
《複雜嵌段高分子的拓撲結構、嵌段序列和微相形態》是依託復旦大學,由邱楓擔任項目負責人的面上項目。項目摘要 發展自洽場理論方法並運用小角X光散射、透射電鏡及原子力顯微鏡等實驗方法,研究複雜嵌段高分子的嵌段序列以及鏈拓撲結構和其微...
第2章 拓撲空間的基本概念 2.1 R的標準拓撲 2.2 拓撲、基與子基 2.3 鄰域、內部與閉包 2.4 可數性 2.5 序列的極限 2.6 子空間 2.7 連續映射 2.8 乘積空間 2.9 商空間與和空間 2.10 拓撲不變數 第3章 基本拓撲...
FCS:Frame Check Sequence,幀校驗序列,實現MAC幀傳送過程中的檢錯及糾錯 TLV(Type、Length、Value),是LLDP報文中最重要的內容,可以有很多種TLV,其中基本TLV如下:當本端設備連線埠啟用LLDP功能後,如果其模式為收發或只發,並且與對...
紐結拓撲 混沌吸引子 符號動力學 混沌時間序列 館藏號 O411.1 唯一標識符 108.ndlc.2.1100009031010001/T3F24.012002627725 館藏目錄 1998\O411.1\28參考資料 1. 奇怪吸引子的拓撲和動力學刻畫及其在混沌時間序列分析中的套用 .國家圖書...
第2章 拓撲空間的基本概念 2.1 R的標準拓撲 2.2 拓撲、基與子基 2.3 鄰域、內部與閉包 2.4 可數性 2.5 序列的極限 2.6 子空間 2.7 連續映射 2.8 乘積空間 2.9 商空間與和空間 2.10 拓撲不變數 第3章 基本拓撲...
針對部分動態可重構系統設計,本項目提出了計算架構和片上網路拓撲生成方法:(1)基於本項目提出的任務調度和布局表示方法——三元序列組,提出了片上網路拓驅動的集成最佳化架構來完成任務調度和布局規劃;(2)基於任務調度和布局規劃的結果...
這種影響主要分三個層面進行:第一層面進行基本分形網路上的分形拓撲符號序列的自動機生成,進而完善地賦予其度量性質(幾何維度、測度等),構成底空間的基本要素;第二層面研究底空間上的微觀隨機運動(離散的隨機行走和連續的布朗運動),...
積拓撲有時稱為點式收斂拓撲,因為:X上的一個序列 (或者網)收斂若且唯若它所有到若且唯若所有Xi收斂。特別是,如果考慮所有在空間X = R對於所有I上的實值函式,在積拓撲上的收斂就是函式的點式收斂。積拓撲的一個重要定理就...
所有一致連續函式都關於引發的拓撲是連續的。完備性 推廣完備度量空間的概念,你也可以定義一致空間的完備性。替代柯西序列,轉而使用柯西濾子(或柯西網)。在一致空間 X上的柯西濾子F是濾子F使得對於所有周圍 U,存在 A∈F有著 A...
