拉梅曲線

拉梅曲線是在笛卡兒坐標系下滿足某特定方程式的點的集合，最初是法國數學家加布里埃爾·拉梅對橢圓的方程進行擴展而得。

定義

拉梅曲線（Lamé curve）是在笛卡兒坐標系下滿足以下方程式的點的集合，方程式為：

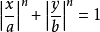
其中，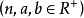

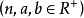
上述方程式的解會是一個在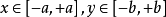的長方形內的封閉曲線，參數a和b稱為曲線的半直徑（semi-diameters）。

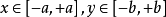
1. 當 0<n<1 時，曲線形狀類似一個四角星，四邊的曲線往內凹；
   
2. 當 n=1 時，曲線形狀為菱形，四個頂點為(±a,0)及(0,±b)；
   
3. 當 1<n<2時，曲線形狀類似菱形，四個頂點位置同上，但四邊曲線往外凸，越接近頂點，曲線的曲率越大，頂點的曲率趨近無限大；
   
4. 當 n=2 時，曲線形狀為橢圓（若a=b，則為圓形）；
   
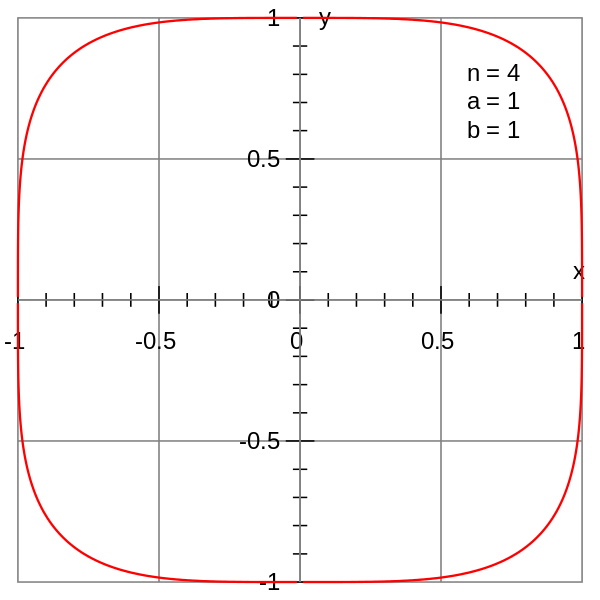
5. 當n>2時，曲線形狀類似四角有圓角的長方形，曲線的曲率在(±a,0)及(0,±b)四點為0；當n=4 時，曲線也稱為方圓形；
   

其它名稱

梅拉曲線也稱為超橢圓（superellipse），n<2的超橢圓稱為次橢圓（hypoellipse），n>2的超橢圓稱為過橢圓（hyperellipse）。