拉克斯一溫德洛夫法(Lax-Wendroff method)簡稱LW法.求解雙曲型方程的一種二階守恆型差分格式.它在雙曲型方程的差分格式發展歷史中有很重要的地位。
對一維雙曲型守恆律方程(組)
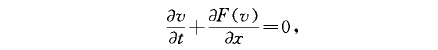
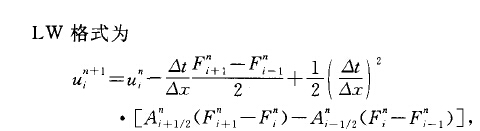
式中n和i分別是t和x方向的節點編號,at和ax._。~_,L_.、___、、_‘,.,.aF.,._、__、.分別是格線時間和空間步長,A } av,當原方程為方程組時A是通量F (v)的雅可比矩陣.
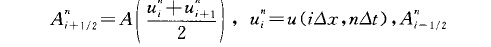
等其他量類似定義.為避免雅可比矩陣A的計算,減少計算時間,里希特邁耶(Richtmyer , R. D.)把LW格式加以改進給出了二步LW格式
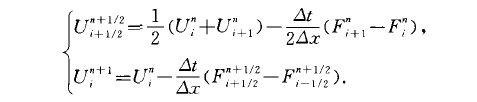
對線性常係數F(z})=Az}情況,一步LW法和二步LW法是完全等價的.在多維情況,二步LW法較之一步LW法優點更明顯.該方法是拉克斯(Lax,P.D.)和溫德洛夫(Wendroff , B.)於1960年發表的.
LW法(Lax-Wendroff method)即“拉克斯-溫德洛夫法”.
