折層法

在分層抽樣中，每層只有一個單位的方差的估計方法。若總體的變異程度很大，則分層可以分列樣本中每層只有一個單位；然而，在這種情況下，對於方差的估計公式就不能計算。為了解決這個矛盾，可以按照事先構想好的方案將層成對的合併，這種方法就稱為折層法。

基本介紹

• 中文名：折層法
• 外文名：Folding method
• 所屬領域：數學
• 本質：分層抽樣
• 特點：每層只有一個單位的方差
• 目的：解決無法汁算方差估計公式

用途

在分層抽樣中，按照事先構想好的方案將層成對地合併的方法，以解決總體的變異程度很大時分到樣本中每層只有一個單位時，無法汁算方差估計公式的矛盾。

計算方法

當每層中只抽取了一個樣本單元時，可以用層間估計量的差異來估計方差，此處僅對總體總量的估計少的方差進行探討，總體均值估計量的方差只需在總體總量的估計的方差的基礎上除以N²即可。

首先將L個層分成G組，每兩個層一組或數層一組。

當層數L為偶數時，兩層分為一組較為合適，共分成G組，此時滿足L=2G，設第j(j=1，2，…，G)組的兩個樣本變數值分別為y_i1和y_i2，由於各層內所採取的是簡單隨機抽樣，所以第j組所包含的兩層的總量估計分別為

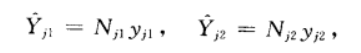
其中N_j1與N_j2分別是這兩層的大小，此時有：

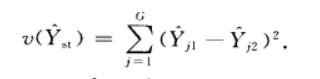
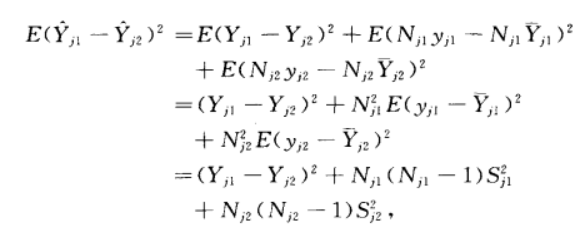
於是：

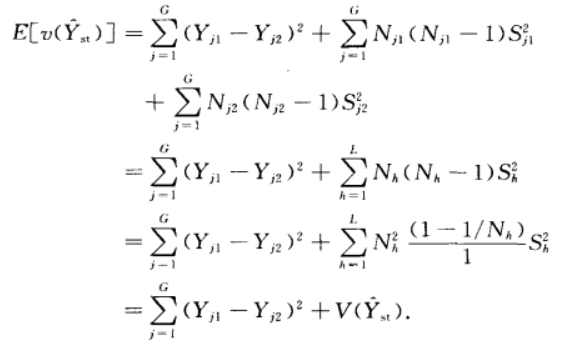
由上式可以看出，要想減小偏倚，就要求在對各層進行分組時，應該儘量將層的總量比較接近的各層劃分為一組，以減小方差估計的偏倚。

類似方法

富勒(Fuller)於1970年提出了構層的方法，該方法使得當每層只抽取一個單位時，方差有了一個無偏的估計，設N/n=N/L=k(為了闡述的方便，假定k為整數)，在1到k這k個數字中抽取一個隨機數r，第一層由編號為r+1到r+k的單位組成，第二層由編號為r+k+1到r+2k的單位組成，依此類推，最後一層(第n層，即第L層)由編號為r+(L-1)k+1到N以及編號為1到r的單位組成，富勒指出，這種方法對於地理分層用區域作單位時效果較好，該方法有一個隱含的條件：彼此相鄰的單位差異程度較小，由於在利用這種方法進行分層的過程中，單位編號有一個首尾相連的過程，當編號為N的單位與編號為l的單位劃歸一層時，要求包含這兩個單位的層內部差異程度較小，對於從編號為1的單位到編號為N的單位取值有上升趨勢的總體來說，採用上面的圓圈形方法(circularmethod)效果較差，因為這種情況下，同時包含第1個單位和第N個單位的層內部差異程度較大，對於這種情況，富勒給出了稍為複雜的另外一種方案，當從編號為1的單位到編號為N的單位取值有上升的趨勢時，該方案有較好的精度，並給出了無偏估計量。