批規範化是指在每次隨機梯度下降時,通過mini-batch來對相應的activation做規範化操作,使得結果(輸出信號各個維度)的均值為0,方差為1. 而最後的“scale and shift”操作則是為了讓因訓練所需而“刻意”加入的BN能夠有可能還原最初的輸入,從而保證整個網路的capacity。
基本介紹
- 中文名:批規範化
- 外文名:Batch Normalization
- 縮寫:BN
背景,簡介,作用,預處理操作選擇,算法實現,BN在CNN中的使用,
背景
2015年深度學習領域,BN出自論文《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》,這個算法當前已經被大量的套用,最新的文獻算法很多都會引用這個算法,進行網路訓練,可見其強大之處非同一般。
深度學習捷報連連、聲名鵲起,隨機梯度下降成了訓練深度網路的主流方法。儘管隨機梯度下降法對於訓練深度網路簡單高效,但是它有個毛病,就是需要我們人為的去選擇參數,比如學習率、參數初始化、權重衰減係數、Drop out比例等。這些參數的選擇對訓練結果至關重要,以至於我們很多時間都浪費在這些的調參上。那么學完這篇文獻之後,你可以不需要那么刻意的慢慢調整參數。BN算法(Batch Normalization)其強大之處如下:
(1)可以選擇比較大的初始學習率,讓你的訓練速度飆漲。以前還需要慢慢調整學習率,甚至在網路訓練到一半的時候,還需要想著學習率進一步調小的比例選擇多少比較合適,可以採用初始很大的學習率,然後學習率的衰減速度也很大,因為這個算法收斂很快。當然這個算法即使你選擇了較小的學習率,也比以前的收斂速度快,因為它具有快速訓練收斂的特性;
(2)再也不用去理會過擬合中drop out、L2正則項參數的選擇問題,採用BN算法後,你可以移除這兩項了參數,或者可以選擇更小的L2正則約束參數了,因為BN具有提高網路泛化能力的特性;
(3)再也不需要使用使用局部回響歸一化層了(局部回響歸一化是Alexnet網路用到的方法,搞視覺的估計比較熟悉),因為BN本身就是一個歸一化網路層;
(4)可以把訓練數據徹底打亂(防止每批訓練的時候,某一個樣本都經常被挑選到,文獻說這個可以提高1%的精度)。
開始講解算法前,先來思考一個問題:在神經網路訓練開始前,都要對輸入數據做一個歸一化處理,那么具體為什麼需要歸一化呢?歸一化後有什麼好處呢?原因在於神經網路學習過程本質就是為了學習數據分布,一旦訓練數據與測試數據的分布不同,那么網路的泛化能力也大大降低;另外一方面,一旦每批訓練數據的分布各不相同(batch 梯度下降),那么網路就要在每次疊代都去學習適應不同的分布,這樣將會大大降低網路的訓練速度,這也正是為什麼我們需要對數據都要做一個歸一化預處理的原因。
對於深度網路的訓練是一個複雜的過程,只要網路的前面幾層發生微小的改變,那么後面幾層就會被累積放大下去。一旦網路某一層的輸入數據的分布發生改變,那么這一層網路就需要去適應學習這個新的數據分布,所以如果訓練過程中,訓練數據的分布一直在發生變化,那么將會影響網路的訓練速度。
網路一旦train起來,那么參數就要發生更新,除了輸入層的數據外(因為輸入層數據,我們已經認為的為每個樣本歸一化),後面網路每一層的輸入數據分布是一直在發生變化的,因為在訓練的時候,前面層訓練參數的更新將導致後面層輸入數據分布的變化。以網路第二層為例:網路的第二層輸入,是由第一層的參數和input計算得到的,而第一層的參數在整個訓練過程中一直在變化,因此必然會引起後面每一層輸入數據分布的改變。我們把網路中間層在訓練過程中,數據分布的改變稱之為:“Internal CovariateShift”。Paper所提出的算法,就是要解決在訓練過程中,中間層數據分布發生改變的情況,於是就有了BatchNormalization,這個牛逼算法的誕生。
簡介
作用
BN也屬於網路的一層。網路除了輸出層外,其它層因為低層網路在訓練的時候更新了參數,而引起後面層輸入數據分布的變化。這個時候我們可能就會想,如果在每一層輸入的時候,再加個預處理操作那該有多好啊,比如網路第三層輸入數據X3(X3表示網路第三層的輸入數據)把它歸一化至:均值0、方差為1,然後再輸入第三層計算,這樣我們就可以解決“InternalCovariateShift”的問題了。
而事實上,paper的算法本質原理就是這樣:在網路的每一層輸入的時候,又插入了一個歸一化層,也就是先做一個歸一化處理,然後再進入網路的下一層。不過文獻歸一化層,可不像我們想像的那么簡單,它是一個可學習、有參數的網路層。
預處理操作選擇
說到神經網路輸入數據預處理,最好的算法莫過於白化預處理。然而白化計算量太大了,很不划算,還有就是白化不是處處可微的,所以在深度學習中,其實很少用到白化。經過白化預處理後,數據滿足條件:a、特徵之間的相關性降低,這個就相當於pca;b、數據均值、標準差歸一化,也就是使得每一維特徵均值為0,標準差為1。如果數據特徵維數比較大,要進行PCA,也就是實現白化的第1個要求,是需要計算特徵向量,計算量非常大,於是為了簡化計算,作者忽略了第1個要求,僅僅使用了下面的公式進行預處理,也就是近似白化預處理:

因此後面我們也將用這個公式,對某一個層網路的輸入數據做一個歸一化處理。需要注意的是,我們訓練過程中採用batch 隨機梯度下降,上面的 指的是每一批訓練數據神經元
指的是每一批訓練數據神經元 的平均值;然後分母就是每一批數據神經元xk激活度的一個標準差了。
的平均值;然後分母就是每一批數據神經元xk激活度的一個標準差了。


算法實現
其實如果是僅僅使用上面的歸一化公式,對網路某一層A的輸出數據做歸一化,然後送入網路下一層B,這樣是會影響到本層網路A所學習到的特徵的。打個比方,比如網路中間某一層學習到特徵數據本身就分布在S型激活函式的兩側,你強制把它給我歸一化處理、標準差也限制在了1,把數據變換成分布於s函式的中間部分,這樣就相當於我這一層網路所學習到的特徵分布被你搞壞了,這可怎么辦?於是作者使出了變換重構,引入了可學習參數γ、β,這就是算法關鍵之處:


是可以恢復出原始的某一層所學到的特徵的。因此我們引入了這個可學習重構參數γ、β,讓我們的網路可以學習恢復出原始網路所要學習的特徵分布。最後BatchNormalization網路層的前向傳導過程公式就是:




公式中m指的是mini-batchsize。
一個網路一旦訓練完了,就沒有了min-batch這個概念了。測試階段我們一般只輸入一個測試樣本,看看結果而已。因此測試樣本,前向傳導的時候,上面的均值u、標準差σ要哪裡來?其實網路一旦訓練完畢,參數都是固定的,這個時候即使是每批訓練樣本進入網路,那么BN層計算的均值u、和標準差都是固定不變的。可以採用這些數值來作為測試樣本所需要的均值、標準差,於是最後測試階段的u和σ 計算公式如下:
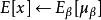

對於均值來說直接計算所有batch u值的平均值;然後對於標準偏差採用每個batchσB的無偏估計最後測試階段,BN的使用公式就是:

BN在CNN中的使用
通過上面的學習,我們知道BN層是對於每個神經元做歸一化處理,甚至只需要對某一個神經元進行歸一化,而不是對一整層網路的神經元進行歸一化。既然BN是對單個神經元的運算,那么在CNN中卷積層上要怎么搞?假如某一層卷積層有6個特徵圖,每個特徵圖的大小是100*100,這樣就相當於這一層網路有6*100*100個神經元,如果採用BN,就會有6*100*100個參數γ、β,這樣豈不是太恐怖了。因此卷積層上的BN使用,其實也是使用了類似權值共享的策略,把一整張特徵圖當做一個神經元進行處理。
卷積神經網路經過卷積後得到的是一系列的特徵圖,如果min-batchsizes為m,那么網路某一層輸入數據可以表示為四維矩陣(m,f,p,q),m為min-batchsizes,f為特徵圖個數,p、q分別為特徵圖的寬高。在cnn中我們可以把每個特徵圖看成是一個特徵處理(一個神經元),因此在使用BatchNormalization,mini-batchsize 的大小就是:m*p*q,於是對於每個特徵圖都只有一對可學習參數:γ、β。說白了吧,這就是相當於求取所有樣本所對應的一個特徵圖的所有神經元的平均值、方差,然後對這個特徵圖神經元做歸一化。下面是來自於keras卷積層的BN實現一小段主要源碼:
input_shape = self.input_shape reduction_axes = list(range(len(input_shape))) del reduction_axes[self.axis] broadcast_shape = [1] * len(input_shape) broadcast_shape[self.axis] = input_shape[self.axis] if train: m = K.mean(X, axis=reduction_axes) brodcast_m = K.reshape(m, broadcast_shape) std = K.mean(K.square(X - brodcast_m) + self.epsilon, axis=reduction_axes) std = K.sqrt(std) brodcast_std = K.reshape(std, broadcast_shape) mean_update = self.momentum * self.running_mean + (1-self.momentum) * m std_update = self.momentum * self.running_std + (1-self.momentum) * std self.updates = [(self.running_mean, mean_update), (self.running_std, std_update)] X_normed = (X - brodcast_m) / (brodcast_std + self.epsilon) else: brodcast_m = K.reshape(self.running_mean, broadcast_shape) brodcast_std = K.reshape(self.running_std, broadcast_shape) X_normed = ((X - brodcast_m) / (brodcast_std + self.epsilon)) out = K.reshape(self.gamma, broadcast_shape) * X_normed + K.reshape(self.beta, broadcast_shape)

