基本介紹
- 中文名：托里切利點
- 外文名：Torricelli point
- 所屬學科：數學（平面幾何）
- 提出者：托里切利(E.Torricelli)
- 相關概念：費馬點，正等角中心
基本介紹,托里切利,
基本介紹
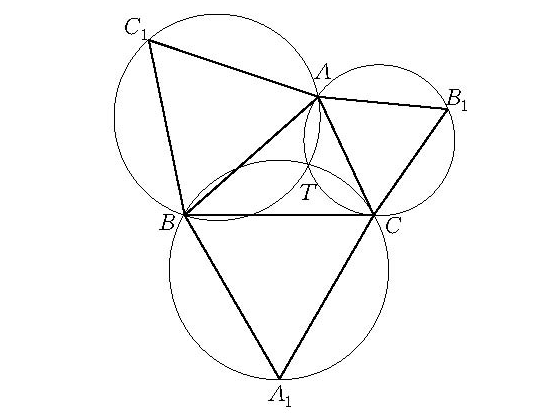
在三角形ABC的三邊AB、BC、CA.上，各向外側作等邊三角形ABC1、A1BC、AB1C，這三個等邊三角形的外接圓交於一點T，我們把點T叫做這一三角形的托里拆里點，而把這三個外接圓叫做托里拆里圓。
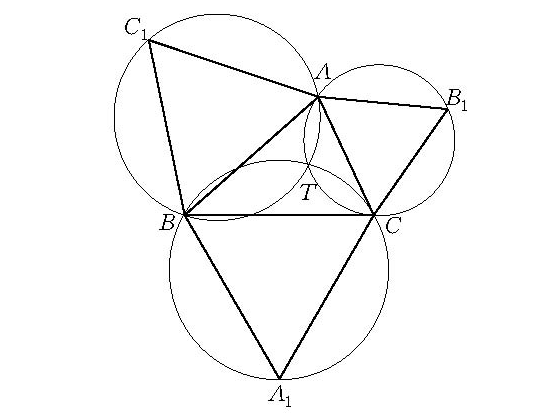圖1 托里拆里點當三角形的三個內角都小於120°時，三角形ABC的托里拆里點T具有如下性質：它到三個頂點的距離之和AT + BT+ CT達到極小。
托里拆里(E.Torricelli, 1608~1647)是義大利物理學家，在一定條件下，托里拆里點和正等角中心、費馬點是一回事，只是托里拆里點是由共點圓來提出問題的，而正等角中心是由共點線來提出問題的，費馬點則是由幾何極值來提出問題的。
托里切利
托里切利(Torricelli，Evangelista)(1608-1647)
托里切利(Torricelli)(1608-1647)托里切利是義大利數學家、物理學家。1608年10月15日生於法恩扎；1647年10月25日卒於佛羅倫斯。
托里切利出生於貴族家庭。1628年開始在羅馬學習數學。在伽利略的著作啟發下，他寫了一篇論文《運動論》，論文引起了伽利略的注意。1641年被邀請到佛羅倫斯會見已經雙目失明的伽利略，並在伽利略生命的最後三個月成為他的秘書和朋友。1642年伽利略去世後，他繼伽利略之後成為佛羅倫斯的宮廷數學家。
托里切利對幾何學的研究促進了微積分的發展，他充分認識到不可分量方法的優點及缺點。他寫的《關於拋物線的維數》是一本很有價值的著作。對拋物線的求積，他提出21個證明，其中10個證明是用古人的方法，其它11個則用了新的不可分量的幾何方法。他在使用不可分量的方法時發現了許多新的結果，並且在靈活和透徹性方面勝於卡瓦列利。托里切利的工作把前人和同時代人所提出的思想和方法，運用得十分精練與嫻熟，以致他的名字在許多情況下都成為爭論優先發明權的焦點。
托里切利還用運動合成來確定任意正整數次冪的拋物線的切線。把這種方法用到瞬時方向的思想，隱含了極限的概念。他通過把瞬時速度的概念滲透到幾何證明中去，從而跨越了經典的傳統論述。他還採用運動合成法求出了阿基米德著作中所提出的一大類曲線的切線。托里切利用幾何方法證明了，一門大炮以相同的初速，但以不同的仰角發射的炮彈的彈道之包絡是一條以炮位為焦點的拋物線。
從托里切利對窮竭法、不可分量法、運動合成法的綜合套用中， 可以發現許多類似於微積分的結論，其中有求曲線弧長、求曲邊形面積、求曲線的切線的一些定理。例如，他證明了：擺線一拱下的面積正好是母圓面積的3倍。特別是，他好象已經認識並套用了：“求切線問題是求面積問題的逆運算”這一規律。遺憾的是，他沒有再前進一步，在這些方法的基礎上建立起普遍適用的一般法則。因而他的工作只差一步便邁進了微積分的重要領域。
托里切利還研究過擺線的性質。他得出了：如果分別以三角形ABC的三條邊AB、BC、CA為邊， 各向此三角形的外側作正三角形ABC1、A1BC、CB1A，則這三個正三角形外接圓交於一點，這個點稱為所給三角形的托里切利點。
托里切利對物理學的突出貢獻是：在《幾何運算》(1644年)一書中，他把動力學的若干著名原理推廣到流體方面；研究過水從容器壁上小洞流出的流量問題；證明了現代教科書上的托里切利原理；對睛雨計的研究使他能把經院哲學中“大自然畏懼真空”這個幽靈趕走，他對玻璃管中為什麼能支持水銀柱的現象給予正確的解釋，並提出可以利用水銀柱高度來測量氣壓。1644年他同維維亞尼(Viviani)：合作製成了世界上第一具水銀氣壓計，一個大氣壓力相當於760毫米高的水銀柱的壓力。為了紀念托里切利，將1毫米水銀產生的壓強定義為1“托”。托里切利研究拋物體運動時，不但得出了拋物體的軌跡是一條拋物線， 而且還猜想出，與水平線成45°角的拋射可以達到最大射程。
