成績常態分配

成績常態分配，一種機率分布的特殊表現形式，在統計某次考試成績分布規律的時候，將成績按分數段製成如右圖類似的統計圖，如果成績分布如右圖所示，中等成績占最多數，其餘成績以中等成績為中軸，向兩側逐次降低，則稱這次成績呈常態分配。

基本介紹

• 中文名：成績常態分配
• 集中性：分布的高峰位於正中央
• 對稱性：左右對稱
• 均勻變動性：分別向左右兩側逐漸均勻下降

主要特徵

1、集中性：成績分布的高峰位於正中央，即平均成績所在的位置

2、對稱性：成績分布的曲線以平均成績為中心，左右對稱

3、均勻變動性：成績分布曲線由平均成績所在處開始，分別向左右兩側逐漸均勻下降

作用

在進行選拔性測驗時（如中考、高考），由於是一種難度測驗,它期望學生的測驗分數呈現常態分配,出現比較極端的分數分布,從而有利於甄別和選拔。因此，分析某次考試的成績分布是否符合選拔性測驗的選拔目的，其中重要參考指標之一就是看成績符合常態分配規律。

評價

常態分配在測驗評價中的功能。

一是對學生進行比較。

呈常態分配的測驗便於選拔優秀,甄別落後。原始分數的比較難以看出個人位置和進步程度。只有將原始分數轉換為標準分數,才具有科學性和客觀性。

二是確定人數和分數線。

測驗成績符合常態分配可以幫助等級評定時確定人數和估計分數段內的人數,確定錄取分數線、各學科的優生率等。

三是確定測驗難度。測驗編制過程中試題難度的確定需要將難易係數根據常態分配機率轉換成難度分數。

過度追求常態分配的弊端。

一是有礙教學質量提高。

過度追求常態分配意味著要求大多數學生成績在70、80分,要有一些90多分和低於60分的。教學實踐中學生成績常態分配成了一種“條件反射”。這樣做的必然結果教學只使少數學生掌握教學內容[2]。對大多數學生如成績達到80分以上,可視為基本達到預定教學目標,應得到認可。如認為不符合常態分配,教師教學效果反而不如多數學生考分在70-80分班級的教師好,這樣做似乎有失公平。

二是不利於激發學生學習動機。

過度追求常態分配實際上強化了部分學生的自卑理,弱化了他們的學習動機和意志品質。因常態分配基於智力常態分配,導致學生成績如何分布似乎是由智商水平決定的,忽略了學生的主觀能動性。即使學生再努力,也無法改變部分人遭遇失敗的命運,這可能造成中下等學生對學習失去信心,缺乏學習興趣和動機。

三是影響測驗真實性。

過度追求常態分配直接導致部分教師急功近利、不負責任地在編制測驗題目和批改試卷上“下功夫”。為達到測驗常態分配,有時教師會降低測驗難度以掩蓋教學質量的低劣;有時人為增加測驗難度會挫傷學生學習積極性,尤其是學差生;有時教師“送出”一些90分以上的分數或將部分學生分數壓到60分以下。這樣,人為製造測驗的不科學、不客觀和不平。

四是違背教育方針。

基礎教育的根本任務是按照我國教育方針,培養德智體全面發展的社會主義事業建設者和接班人。過度追求常態分配強行製造學差生,有悖教育方針和素質教育思想。從某種意義上看,成績的常態分配實質上並不是教育的成功,而是失敗[3]。

正態曲線並不是神聖的東西。而是適用於偶然與隨機活動的分布。教育是一種有目的的活動,我們力圖使學掌握所教授的事物。如教學有成效,成績分布應當與常態分配很不相同。事實上甚至可以斷言:成績分布接近常態分配時,說明我們的教育努力不成功[4]。

例子

用例

各種競賽性測驗和擇優錄取的升學測驗等都屬於選拔性測驗。

案例

（柳州三中 鐘東華 )

記得大學畢業剛開始做老師的時候，對很多東西都不懂。其中就有一個在教學過程中遇到的問題使我困惑了很久。

期末考試剛剛把試卷改完，統計好分數，我就拿到班上去講評了。由於是流水改試卷，難免就有幾個同學是得59分的，於是問題就出來了。有一個同學剛好考得59分，於是他就跟我說：“老師，你給我加一分可以嗎？”“為什麼要給你加一分呢？”我疑惑道。“加上一分我能就及格了。”他渴望道。我解釋道：“分數並沒有加錯啊！”“可是您看，我這裡是可以得一分的，你沒給呢？”“這種情況統一不給的。這都是流水改卷呢！”他哀求道：“過年了，加一分就能及格了，也好和父母交待，也好過個好年啊。”我拗不過他，只好說：“那好吧，我給你加一分吧，但是希望你下次能努力一點，考個好成績。”

看著他欣喜若狂的樣子，我真不知道自己所做的是對還是錯。也許是我的私心，也許是為了對別的學生也公平一些，事後我把其它59分的都加到了60分，於是學生的成績及格了，當然我所教科目的及格率也得到了相應的提高，這樣我們皆大歡喜，同時也辟免了師生相互之間就試卷中能不能加這一分的爭論。雖然我把學生的成績加到了及格，但是我心理仍就期望他應該會吸取教訓，從今往後認真學習，從而考出好的成績。可是這也只是我的一廂情願，隨著下一次考試的到來，由於學習難度的加深，他非但沒有前進一步，反而更退一步了，更別說有資格來求我加一分了。那些曾經加了一分的同學也沒能達到我所期望的及格分數。這一出乎我期望之外的情況使我陷入了深深的困惑之中，加這一分對學生來說到底有沒有用？

本來流水改試卷已經很科學了，但我卻畫蛇添足般的給59分的同學加上一分，從而違背了科學原理。這難道不值得我深思嗎？

直到有一次我在教務處做學生考試成績分析時，我才恍然大悟。

從統計學的角度來說,學生的考試成績是近似服從常態分配的。常態分配是機率論中的最重要分布。大量的實踐與理論分析均表明，大多數隨機變數均服從或近似服從常態分配。如測量的誤差，學生的考試成績；人的身高與體重；產品的質量數據，投資的收益率等等均可認為服從常態分配。常態分配的隨機變數套用範圍之廣, 其在數理統計學中占有極其重要的地位，可以說任何一個隨機變數不可能與之相比。現今仍在經常使用的許多統計方法，就是建立在“所研究的量具有或近似地具有常態分配”這個假定的基礎上，而經驗和理論（機率論中所謂“中心極限定理”）都表明這個假定的現實性。現實世界中許多現象看起來是雜亂無章的，但在紛亂中卻又有一種秩序存在。研究表明，若影響某一數量指標的隨機因素很多，而每一種因素所起的作用又不太大，在理論上可以證明，該數量指標是服從常態分配的。因此我們可以得出結論，由於學生的考試成績是近似服從常態分配的，所以存在59分是很正常的，如果沒有則不正常了。

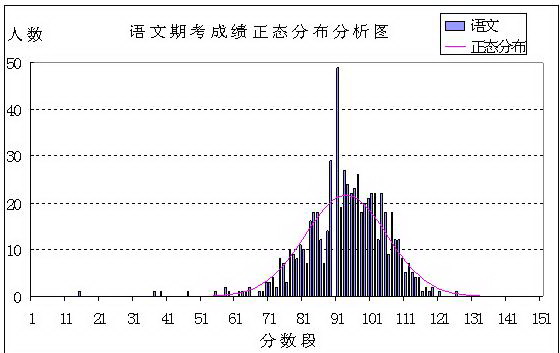
我們來看這樣一個例子。期考語文的“常態分配曲線”（Normal Distribution Curve）：

圖中紅色的光滑曲線是由該次語文考試的平均分和標準方差所決定的常態分配曲線，而柱狀圖部分則是該次考試的實際人數分布（由於EXCEL電子表格的強大計算能力，我們可以計算出每一分數段的實際人數）。語文滿分150分，90分算及格（橫坐標的分數段部分是從0分到150分進行統計，共有151個單位）。通過圖中的柱狀圖分布來分析，我們完全可以看出89分這一格人數完全為空，90分這一格的人數飈得老高，可以看出89分的人數全部都跑到90分的人數了。通常來說，某一分數段的人數為空，是很正常的，但是它鄰近的這一分數段卻升得老高，這就不正常了，就說明有人為的改動了。所以我們要嚴格統計學生的成績，實事求是的分析學生的成績情況，從而才能找出教學中所存在的原因。這樣才能制定出下一步的教學改進計畫，為進一步改善學生的知識結構做好準備。通過學生的考試成績的常態分配圖，我們可以分析出學生成績是不是存在著兩極分化（兩頭大的情況）、或者通過了解學生成績的分布狀態，為下一步制定相應的教學策略做好準備等等。所以，從統計學的角度來說，我確實不應該給學生加這一分。

從學生的角度來說，學生的個體差異性也決定了“加一分”不能成為一種普遍使用的策略。給學生“加一分”，從表面上看，是期望通過給學生一個及格的分數來促進學生積極地去學習，實際上正是由於這一行為所蘊含的對學生的尊重與信任，從而真正的激活了學生學習的主體精神，是師生之間的一種積極的情感效應。如果沒有真正激活學生學習的積極性，而只是為了滿足學生心理上的某種特殊需求，那對學生的學習是毫無益處的。對於一個上進心強的，渴望取得好成績的學生，這一策略可能很有效，能夠激勵他奮起學習，但是對於一個進取心不強，考試只在乎分數而不在乎知識掌握的學生，給他加再多的分數，恐怕也是愛莫能助。而且這種策略面向某個特殊個體時，有針對性地隨機使用，可能效果頗佳；如果擴大為面向全體，頻繁地使用，效果就會逐漸降低，最終變為一種讓學生毫無感覺的、形式化的東西。因此，給學生“加一分”，這只能是一種隨機性的“教育機智”，而不能作為一種“教育機制”來普遍使用。

當我再次遇到這種情況時，我會微笑著鼓勵他：“只要你認真、努力地學習，下次肯定能及格。”因為我知道這一分所蘊含的道理，我再也不能輕易的給他加這一分。我只能在心裡期待著他能夠幡然醒悟，通過自己真正的努力來爭取這一分，而不是再拿這一分來自欺欺人。