基本介紹
- 中文名：惠特克函式
- 外文名：Whittaker function
- 學科：數學
- 任務：惠特克
- 定義：解惠特克方程時出現的特殊函式
定義,級數展開,
相關詞條
- 惠特克函式
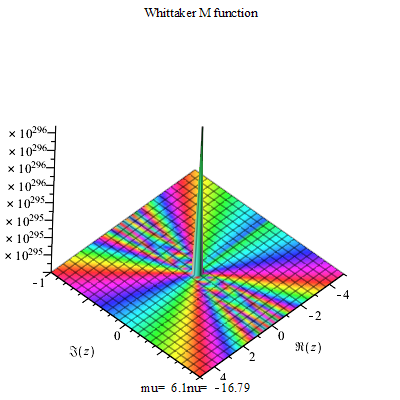
惠特克函式（WhittakerM function），是解惠特克方程時出現的幾個特殊函式，是Whittaker（1904）引入的合流超幾何函式的一種修改形式，使涉及解更對稱的公式更為合理。定義惠特克函式，惠泰克1904推...
- 拋物函式
中文名 拋物函式 外文名 parabolic function 所屬學科 數學 別名 旋轉拋物面函式 定義 在旋轉拋物面坐標系中求解波動方程時出現的一類特殊函式 它們是微分方程的解,可用惠特克函式從 , ( z)和Wk. ,(z)表示:因此,這些函式的性質可以...
- 特殊函式(數學術語)
二十世紀對特殊函式理論興趣正濃。惠特克和沃森（1902）的經典教科書試圖通過使用複雜的變數來統一理論；G. N. Watson將貝塞爾功能理論技術儘可能地推廣到一種特別允許漸近研究的重要類型。後來的貝特曼手稿項目，在亞瑟·埃里迪亞（Arthur...
- 誤差函式
的誤差函式定義為：且有erf(∞)=1和erf(-x)=-erf(x)。互補誤差函式erfc(x )定義為：數學表達 誤差函式是特殊的不完全伽馬函式之一.即 也可以用匯合型超幾何函式F(α;γ;z)或惠特克函式W(z)表示：導數與積分 誤差函式的導數...
- 拋物柱面函式
對於a的整數值，這些（即U和V）可以用Hermite多項式來重新表示；或者，它們也可以用貝塞爾函式來表示。函式U和V也與拋物柱面函式Dp（x）（可追溯到Whittaker（1902）的符號）有關：函式D（a，z）由惠特克和沃森引入，可以用超幾何函式...
- 餘弦積分
餘弦積分 餘弦積分(cosine integral)是由積分定義的一種特殊函式。它在除去負實軸(一2，0)的z平面上單值解析，可以表示成惠特克函式Wk.,n (z)或不完全伽馬函式L(v,z):
- 通信接收機:DSP、軟體無線電和設計(第三版)
2.2.3 傳遞函式 82 2.2.4 信道衝激回響的時間回響和傳遞函式 83 2.3 無線電系統的實現 85 2.3.1 輸入特性 85 2.3.2 增益、靈敏度和噪聲係數 86 2.4 選擇性 90 2.5 動態範圍 91 2.5.1 減敏度 93 2.5....
