恆熱流

對恆熱流加熱條件下物體表面的燒蝕過程進行近似理論分析計算。燒蝕過程中的燒蝕界面位置隨時間移動，其位置未知且是解的一部份，在移動的界面上須滿足能量平衡條件。將燒蝕過程分為物體的預熱使加熱表面達到熔解溫度階段和開始燒蝕階段，分別對兩階段的溫度場進行理論分析，利用移動界面上的能量平衡條件，建立燒蝕移動界面的運動控制方程。

基本介紹

• 中文名：恆熱流
• 外文名：Constant heat flow
• 描述：加熱條件
• 套用：能量平衡理論計算
• 學科：熱力學

概念

大多數燒蝕過程是表面熱流恆定的過程，作者從傳熱模型出發，針對恆熱流加熱的表面燒蝕過程的導熱微分方程進行了近似理論分析，建立了燒蝕移動界面的運動控制方程。利用一階非線性常微分方程，與分析解相比，方程形式簡單，且一階非線性常微分方程的解法十分成熟，例如RUNGE—KUTTA方法，可獲得準確的數值解。
計算了在不同熱流條件下燒蝕界面的移動規律，該方法可方便地套用到其他特定加熱條件下的理論求解。

恆熱流加熱條件下燒蝕過程的解

燒蝕過程在機械加工、金屬表面的處理、雷射打孔、金屬材料的切割、與焊接等諸多領域有著廣泛的套用。燒蝕過程的快慢不僅與熱源的強度有關，還與被燒蝕的材料特性、傳熱過程有著緊密的聯繫。燒蝕過程的顯著特點是其表面發生的相變過程，使研究區域具有一個隨時間變化、位置待定的移動界面及其由此產生的計算區域的變化。邊界條件的非線性，使得該類問題的求解較為困難。已有的近似解法主要有積分近似解、焓方法、攝動解
等。例如在攝動解中，雖然考慮了預熱、加熱兩階段，但其級數解超過兩階以後變得過於冗長、複雜。也有極少數的分析解，但其表達式也是過於冗長，不便套用。為尋找簡便可行的算法，且考慮到大多數燒蝕過程是表面熱流恆定的過程，從傳熱模型出發，針對恆熱流加熱的表面燒蝕過程的導熱微分方程進行了近似理論分析。

燒蝕過程的物理模型及分析解

將燒蝕過程分為兩個階段來處理，第一階段為預熱階段，過程開始以常熱流密度q_o對物體加熱，將物體表面溫度提升到熔解溫度。第二階段為燒蝕過程，在該過程中，假設被燒蝕掉的物體快速離開物體表面，燒蝕界面在向物體內部傳導熱量的同時由界面處帶走熔解潛熱。由於在大功率熱流的作用下溫度的變化主要發生在沿熱流的方向，因此可以近似認為傳熱過程是一維的。

考慮一厚度為L、初始溫度為T₀的物體(圖1)，一側以熱流密度為q₀的恆熱流對其加熱，假設物體的另一側絕熱，各物性參數取常數。物體加熱側表面達到熔解溫度後開始燒蝕過程。前面已假設被燒蝕掉的物體快速離開物體表面，燒蝕的物體表面時刻暴露在加熱環境下。伴隨著燒蝕過程，其熱量一部分由物體的熔解潛熱吸收帶走，一部分向物體內部導熱傳遞，燒蝕界面的溫度為材料的熔解溫度露且保持不變，以燒蝕過程的開始作為時間起點，取常物性。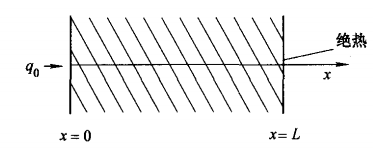

圖1 預熱階段導熱過程示意圖

結果討論

對恆熱流加熱條件下物體表面的燒蝕過程進行了近似理論分析計算，通過將燒蝕過程分為預熱階段和燒蝕階段考慮，建立了燒蝕移動界面的運動控制方程並計算了在不同熱流條件下燒蝕界面的移動規律。利用該方程可方便地確定任意時刻的燒蝕進度，為燒蝕過程的控制提供理論依據。該方法可方便地推廣到其他特定加熱條件，例如能使導熱方程具有解析解的邊界條件的燒蝕計算。

恆熱流工況下強化傳熱管傳性能的評價

強化傳熱技術廣泛套用於工程實際中，國內外學者相繼研製出了多種新型強化傳熱元件，如螺旋槽管等，並對其流動與傳熱特性進行了大量的實驗研究。但在眾多的強化傳熱元件中，如何選擇合適的換熱管，即如何綜合評價其性能是一個有待進一步研究的問題。工程上套用最廣泛的是Webb以熱力學第一定律為基礎提出的強化傳熱性能評價方法，但該方法未能區分出傳熱量和動力消耗之間的能質差別；Bejan以熱力學第二定律為基礎，從不可逆損失角度出發，提出了用強化前後熵產率相對大小作為性能比較的判據，該判據雖然克服了Webb方法的不足，但不易於在工程實際中具體套用。

對動量、質量、熱量傳遞的動力學規律已經作了深入和廣泛的研究。實質上，動量、質量、熱量傳遞及任何其它形式的傳遞現象，其共同本質是能量和㶲的傳遞和轉換。對對流換熱過程，溫度場和壓力場（速度場）有著直接影響對流換熱效果的耦合關係。如認為主導勢場為溫度場，且用勢差代替勢場梯度。

在恆熱流工況下分析了各參數對強化前後管內對流換熱過程傳㶲性能的影響，提出了強化前後平均㶲傳遞之差或傳㶲量之差作為強化傳熱性能評價指標，通過分析得到強化管結構參數對管內對流換熱的㶲傳遞有重要的影響。

U型埋管傳熱數值模擬及恆熱流模型分析

地熱能源是一種綠色、清潔並可以循環使用的新型可利用能源。基於地熱能源的各種優點和國家戰略能源方向的轉移，以開發利用地熱資源為目的地源熱泵技術在我國得到迅速發展。地源熱泵工程主要採用垂直的U型埋管作為換熱器，因而對於這種U型管換熱器模型的研究就顯得非常有意義。儘管，國內外對地源熱泵地埋換熱器與土壤傳熱數學模型的研究已經有幾十年的歷史了，但是還沒有一種普遍公認的模型。工程實踐中經常使用的是線熱源模型和柱熱源模型，兩種模型都將U型管內流體假定為恆定熱源，從不同的角度對鑽孔內的傳熱進行近似。

地源熱泵中，地下埋管周圍的土壤溫度場分布狀況十分重要。因為只有充分了解土壤溫度場在地源熱泵運行前後的分布情況，才有可能設計出最優的地下埋管換熱器、埋管形式、埋管間距、數量以及布局。實驗研究埋管周圍溫度場的變化十分準確，但經濟成本較高，在實際工程中受到了限制。隨著計算機技術的飛速發展，通過建立埋管換熱器傳熱模型，並藉助數學方法和數值分析軟體對埋管周圍土壤溫度場進行模擬分析的技術，由於可以
較準確地了解埋管換熱器對周圍土壤溫度場的影響而得到了快速發展。但以往的數值模擬往往忽略了U型管材料對溫度場的影響，並且幾乎沒有學者或技術人員分析過工程實踐中常用的線源模型與柱源模型那個更具利用性。

U型埋管傳熱二維數值模擬

U型埋管換熱的二維數值模型基本上都是將U型管考慮為等價管(當量直徑)，假定管壁與土壤之間的熱流恆定，利用Matlab軟體的PDE工具箱進行模擬，忽略了鑽孔及其回填材料熱物性對模擬溫度場的影響，採用Matlab中PDE工具箱進行模擬，但建立考慮實際鑽孔半徑和回填材料的U型埋管的二維換熱數值模型，仍將U型管考慮為等價管(當量直徑)，管壁與回填材料之間熱流恆定。建立非穩態模擬恆熱流條件下72h內鑽孔壁溫度變化，並與線源模型和柱源模型所得結果進行對比分析。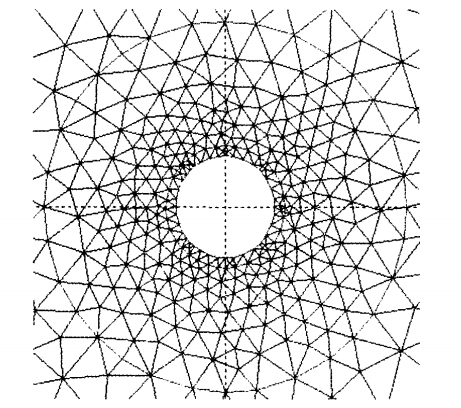

回填材料的格線劃分

圓柱熱源模型就是將鑽孔，包括埋管和回填材料看作土壤中的均勻圓
柱狀熱源，並假設鑽孔壁處有一恆定熱流。在這一模型中，以鑽孔壁為界，考慮了鑽孔回填部分和大地土壤存在差異，但卻忽略了鑽孔內材料的熱容量
而把管內流體的加熱熱流瞬時地施加到孔壁上，這種模型實際上也是從另一個角度對鑽孔內的傳熱進行近似。

結果分析

足夠長的時間情況下，線源模型和柱源模型計算結果與數值模擬結果擬合的越來越接近，線源模型在15h左右便可十分接近於數值模擬結果柱源模型則需50h以後才能十分接近於二維數值模擬結果。線源模型計算結果僅在初始階段低於數值模擬結果，基本上計算孔壁溫度低於或等於數值模擬結果，而柱源模型計算孔壁溫度始終高於數值模擬結果，而且線源模型計算孔壁溫度低於柱源模型計算孔壁溫度。

線源模型計算孔壁溫度更接近於數值模擬結果，說明線源模型對U型埋管傳熱模型的簡化相比柱源模型接近實際情況，工程中可以加以利用。在土壤溫度場穩定後，線原模型與柱源模型相比，儘管線原模型更接近實際情況，但是二者的誤差百分比與工程允許誤差5%以內相比很小。因而，在工程勘探設計中，無論是採用線源模型還是柱源模型對工程設計不會帶來大的影響。