恆向線是地球上兩點之間與經線處處保持角度相等的曲線，是天文學專有名詞。恆向線航線不是航程最短的航線，但卻是操作極為方便的單一航向航行的航線，即在墨卡托海圖上從起始點到目的點的一條直線。在低緯度或航向接近南北時，它和大圓航線的航程差別很小。
船舶大洋航行有四種航線，即:大圓航線、恆向線航線、等緯圈航線和混合航線。其中等緯圈航線為恆向線航線的特例，混合航線為大圓航線和等緯圈航線的結合。
基本介紹
- 中文名：恆向線
- 外文名：loxodrome
- 所屬學科：天文學
- 套用：導航
- 定義：與經線處處保持角度相等的曲線
- 特例：等緯圈航線
恆向線簡介,航線分類,精確計算,高精度算法,
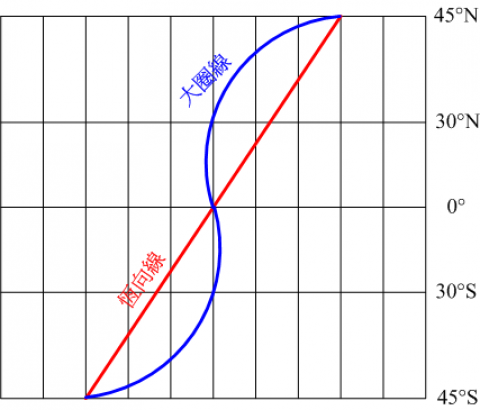
恆向線簡介
恆向線是地球上兩點之間與經線處處保持角度相等的曲線，是天文學專有名詞。恆向線航線不是航程最短的航線，但卻是操作極為方便的單一航向航行的航線，即在墨卡托海圖上從起始點到目的點的一條直線。在低緯度或航向接近南北時，它和大圓航線的航程差別很小。
通常比大圓航線要長，當距離較短時二者差別不大。當等角航線與經線或赤道重合時，等角航線與大圓航線的方向、距離相等。在墨卡托投影地圖上，等角航線是一條直線，故在航海中常用墨卡托投影地圖繪算航跡，計算航線等。在其他投影地圖上，等角航線都是曲線。
航線分類
船舶大洋航行有四種航線，即:大圓航線、恆向線航線、等緯圈航線和混合航線。其中等緯圈航線為恆向線航線的特例，混合航線為大圓航線和等緯圈航線的結合。
大圓航線即基本沿著兩點間大圓弧航行的航線。這是兩點間地理航程最短的航線，特別是在高緯度海區航向接近東西，橫跨經度較大時，大圓航程比恆向線航程要短達數百海里。但是，由於大圓弧和所有子午線相交角度不等，如果嚴格沿大圓弧航行，則必須不斷改變航向。
恆向線是船舶始終按恆定的航向航行的航線，也叫等角航線。恆向線是地球上兩點之間與經線處處保持角度相等的曲線。通常比大圓航線要長，當距離較短時二者差別不大。當等角航線與經線或赤道重合時，等角航線與大圓航線的方向、距離相等。在墨卡托投影地圖上，等角航線是一條直線，故在航海中常用墨卡托投影地圖繪算航跡，計算航線等。在其他投影地圖上，等角航線都是曲線。
精確計算
船舶航行時為了便於操縱只能採用恆向線航線，恆向線在墨卡托海圖上表現為直線，但實際在地球表面上一般為球面螺旋曲線。航跡計算是指恆向線的航跡計算，其目的，一是根據航行起始點的經、緯度和船舶的航向、航程求算出到達點的經、緯度；二是根據起航點和到達點的經緯度求取航向和航程。在目前實際航海套用中，套用較多的是後一種，在制定航行計畫時，先在海圖上確定轉向點(way point),後製作航線表。而船載GPS一般僅有大圓航線的航向和航程數據。隨著計算機在船上的廣泛使用，利用EXCEL等工具編寫公式自動生成航線表，可給工作帶來很大的方便。所採用的航跡計算方法有幾種，採用的數學方法不同,計算精度和計算的複雜性亦不同。利用以地球圓球體為基礎的平均緯度航法較為簡單，但只適合於赤道一側的航跡計算，而且精度不高，在簡單計算中較為實用。將地球作為地球橢圓體的墨卡托航法精度最高，計算方法也最複雜，對於跨赤道的航行可採用墨卡托航法，但這種方法的計算段較欠缺。
大連海事大學的胡江強等以地球橢圓體為基礎，已知起航點經緯度(φ1,λ1)和到達點經緯度(φ2,λ2)，通過較詳細的理論公式推導，得出了船舶東西向航行、南北向航行及其他航向航行時恆向線航線的航向和航程的精確計算數學模型，為計算機自動計算提供依據。航向均以圓周法度量，航程均以法定海里為單位度量。他們的航跡計算數學模型有較廣泛的適用性，無論赤道一側航行或跨赤道航行均能適用。
高精度算法
為便於船舶操縱，在航程不太長、緯度不太高海區，採用兩點間的恆向線航法.在航程較長時，需根據實際情況將大地線或大圓航線分成若干段,每一段再採用恆向線航法。恆向線或等角航線在地球表面上為一條與所有子午線成等角、具有雙重曲率且形狀如螺旋的空間曲線，在墨卡托投影平面上表現為直線。恆向線主題解算算法包括航海上精度要求較低，適於手工計算的實用公式，如中分緯度算法；適於電算化且精度較高的算法，如趙俊生的恆向線主題正反算，但該算法不通用且反算時需疊代；李厚朴的恆向線主題正反算，在航向為270°時，正解中到達點經度和反解中恆向線長度計算公式均不成立，且反解計算航向角時需要進行象限判定。
恆向線主題解算的關鍵為等距離緯度和等量緯度的正反解。楊啟和套用Lagrange級數推導出數值形式的直接展開式,但其精度低且難記憶;邊少鋒給出含e的8次方項展開式。
