德魯克－普拉格準則

德魯克－普拉格準則是反映岩土材料強度的準則，其由德魯克和普拉格於1952年提出。

基本介紹

• 中文名：德魯克－普拉格準則
• 外文名： Drucker-Prager  

關於強度準則

強度準則的建立是為了反映岩石的破壞機理。岩石的破壞，通常可以分為脆性破壞和延性破壞。前者特點是岩石達到破壞時不產生明顯的變形，後者的特點是破壞時會產生明顯的塑性變形而不呈現明顯的破壞面。岩石之所以能產生脆性或延性破壞，除了受到應力及應力狀態影響外，也受到溫度、應變率，地質構造等因素的影響，但大多數岩石破壞準則僅僅認為與應力或應變狀態有關。在單向應力狀態時，岩石破壞準則可以直接通過岩石力學實驗獲得。例如採用破壞時的最大應力作為破壞判據，但一般在地層中，岩石是處於三向應力狀態的，而岩石的破壞往往與三個主應力大小及其相互間的比值有關。

德魯克－普拉格的岩石破壞準則

M-C準則體現了岩土材料壓剪破壞的實質，所以獲得廣泛的套用。但這類準則沒有反映中間主應力的影響，不能解釋岩土材料在靜水壓力下也能屈服或破壞的現象。

德魯克和普拉格於1952年提出了考慮靜水壓力影響的廣義Mises屈服與破壞準則，常常被稱為德魯克－普拉格準則,簡稱D-P準則，即：

式中， 為應力的第一不變數；

為應力偏量第二不變數；α，K為與岩石內摩擦角和粘結力有關的實驗常數。

D-P準則計入了中間主應力的影響，又考慮了靜水壓力的作用，克服了M-C準則的主要弱點，已在國內岩土力學與工程的數值計算分析中獲得廣泛的套用。

德魯克-普拉格岩石強度準則的修正

德魯克一普拉格準則岩石力學中最為重要的強度理論之一，在岩土工程研究中，尤其是在岩土工程數值分析中套用極為廣泛，該強度理論同時反映了體積應力、剪應力和中間主應力力對岩石強度的影響，較比它強度理論更能反映實際。然向，工程實際套用表明該強度理論較為保守，以此作為依據進行工程設計計算，，其經濟性值得考慮，有必要對該強度理論進行合理修正。

本構模型的建立

利用Lemaitre J[9]應變等價性假說，可以建立岩石損傷本構關係

式中：[C]為岩石材料彈性矩陣；[σ*]為有效應力矩陣；[σ]為名義應力矩陣；[ε]為應變矩陣；D為岩石損傷變數。

過去大多用岩石軸向主應變來表示岩石微元的強度[3,4]，作者認為它不能反映複雜應力狀態對岩石微元 強度的影響。因此，基於Drucker-Prager破壞準則，提出岩石微元強度F*的表示方法

式中：α為與岩石粘聚力c和內摩擦角φ有關的參數,I*1為應力張量的第一不變數，I*1=σ*1+σ*2+σ*3；J*2為應力偏量的第二不變數，J*2=[(σ*1-σ*2)^2+(σ*2-σ*3)^2+(σ*1-σ*3)^2]/6，σ * 1、σ*2、σ*3為有效應力。

本構模型的修正

不同的圍壓或者不同的複雜應力狀態對岩石破裂過程損傷本構關係的影響是不同的，為了使上述所建 立的模型具有一般性，必須對此模型進行修正，其修正方法必須反映岩石應力與應變關係曲線的特點，因此有必要探討前述岩石損傷統計本構模型參數的變化規律。

參數F0與S0反映了岩石變形的力學性質，如圖2、圖3所示。由圖中可以看出：(1)岩石的應力應變曲線 的峰值隨F0與S0的增大而增大，但是，F0與S0的變化並不改變峰值前線性變形曲線；(2)F0與S0對岩石應力應 變曲線的非線性變形部分，尤其是峰值後曲線影響是明顯的，可以改變曲線的形態。上述兩個特點反映了 F0與S0對岩石應力應變曲線的影響。

圖2 圖3

大量試驗曲線表明，不同圍壓下岩石全應力應變曲線存在如下普遍特點：(1)岩石全應力應變曲線的 峰值隨圍壓的變化而變化，峰值前應力較高的非線性部分與峰值後軟化曲線部分同樣隨圍壓變化而變化； (2)峰值前低應力線性部分並不隨圍壓的變化而變化。對岩石損傷軟化統計本構模型進行修正也必須反映 上述特點。

對比前述得到的F0、S0對岩石損傷統計本構模型影響的特點與規律，可以看出，如果能建立起F0及S0 與圍壓σ3的關係，那么就能比較有效地對岩石損傷統計本構模型進行修正。考察根據前述方法得到的文獻(周維垣，吳澎，楊若瓊.節理岩體的損傷模型[A].岩石力學新進展[C].瀋陽：東北工學院出版社,1989. )中不同圍壓下岩石應力應變試驗曲線的統計損傷本構方程參數F0與S0，如果分別以F0與S0為縱坐標，圍 壓σ3為橫坐標，即可得到F0-σ3與S0-σ3散點分布圖，見圖4和圖5。

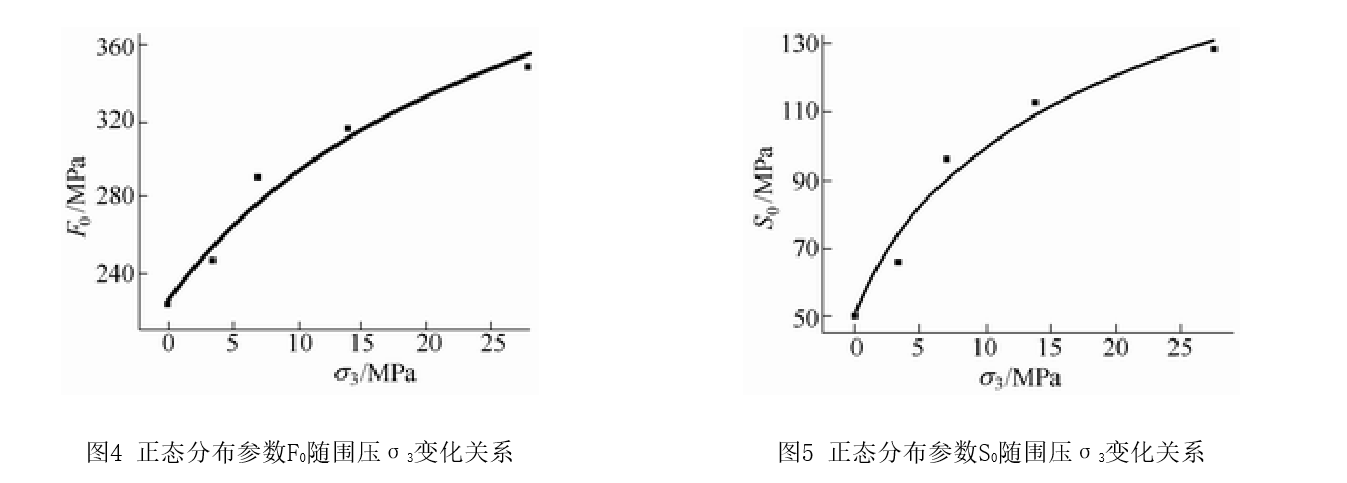
圖4