循環功率

循環功率是指兩端電壓的差值和環網總阻抗的功率。在兩端電壓不相等的兩端供電網路中，各線段中流通的功率可看作是兩個功率分量的疊加。其一為兩端電壓相等時的功率；另一為取決於兩端電壓的差值和環網總阻抗的功率，稱循環功率。在多橋驅動汽車中，循環功率也稱為寄生功率。

基本介紹

• 中文名：循環功率
• 外文名：循環功率
• 描述：兩端電壓差值和環網總阻抗的功率
• 套用：多橋驅動汽車
• 學科：物理

概念

在兩端供電網路中，每個電源點送出的功率都包含兩部分，第一部分有負荷功率和網路參數確定，每一個負荷的功率都以該負荷點到兩個電源點間的阻抗共軛值成反比的關係分配，而且可以逐個地計算。第二部分與負荷無關，它可以在網路中負荷切除的情況下，由兩個供電點的電壓差和網路參數確定，通常稱這部分功率為循環功率。當兩電源點電壓相等時，循環功率為零。

多軸驅動車輛循環功率的計算

理論研究證明多軸驅動車輛由於多個驅動輪支撐整車的重量，輪胎總的接地面積增大，輪胎的實際變形減小，從而能增加汽車的牽引力，提高其動力性能、通過性能、燃油經濟性能、操縱穩定性能和交通安全性能。然而在實踐中，某些多軸驅動車輛的這種優勢表現得並不明顯。這是什麼原因呢?是由於不合適的驅動力分配導致各驅動車輪之間的功率循環造成的。所謂功率循環，也即寄生功率，是指各驅動車輪由於運動狀態不一致而引起的功率損失。

循環功率計算方法

循環功率涉及的因素較多，為了簡化計算作如下假設：汽車處於勻速行駛狀態；車架的剛度遠大於車輪和懸架系統的剛度；同一驅動橋左右兩側的軸荷相同；輪胎具有相同的滾動半徑，並且各車輪的附著係數相同；前後車輪的特性係數相同。功率循環既然是驅動功率的因分配不合理而造成的損失，那么其理論上的大小應該是在某一特定的力矩、速度下驅動功率獨立作用在單個車輪上的功率和減去扭矩整體作用在單個車輪的功率和。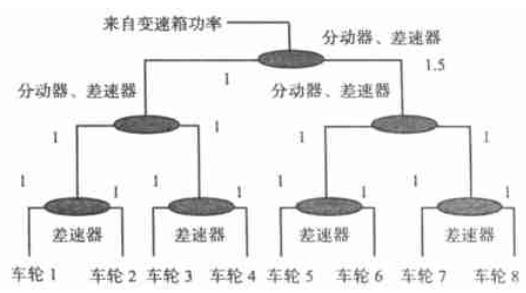

傳動系功能

國外對於寄生功率尚沒有完整的計算依據，現根據近期的研究和試驗提出如下的計算方法。現以某輛載貨車(8×8)為例計算，整車的基本技術參數如下：一級分動器的扭矩分配比為1∶1.5；其它分動器、差速器的扭矩分配比都是1∶1；軸距1750+3800+1750mm；總質量38t；重心距一橋3650mm，高1732mm；滾動半徑為630mm；最高車速72.5km/h；最高車速下的發動機的輸出功率為300kW。不考慮結構而把差速器僅當成一種實現動力分配的功能裝置，確定在分配到各個驅動車輪上的驅動扭矩。

研究結論

通過分析得出：循環功率是由於扭矩分配不合理造成的。當各個車輪所獲得的扭矩與車輪的軸荷相匹配時，循環功率為0，傳動效率最大(為100%)；當至少有一個車輪打滑時，循環功率所占總功率的比例逐漸增大，傳動效率逐漸降低，特別當整車打滑時，傳動效率為0。

行星傳動變速箱功率流及循環功率分析法

對行星傳動進行功率流及循環功率的分析是評判行星傳動機構性能的一項不可缺少的步驟。以往對此問題的分析方法是以三角形分析法為主。如圖1所示在某擋條件下的雙行星排變速傳動(圖中：ω₀、M₀分別為輸入角速度和輸入功率，ω_∞、M_∞分別為輸出角速度和輸出功率。α₁、α₂分別為第1行星排和第2行星排的排參數)

圖1 雙行星輪機構

三角形分析法在套用過程中，存在著分析過於複雜，不易理解等問題。且不能快速、準確地計算出功率流的大小。針對此現象，介紹一種快速、簡便、易懂的功率流分析法—節點分析法。

節點分析法

(1)功率輸入、輸出的基本原則

如圖2所示，對於系統的輸入功率具有輸入角速度ω₀與輸入扭矩M₀同向的特點。因此，當某一構件上的角速度與自身扭矩同向時，可認為流經該構件的功率為向系統內輸入功率。同理，當某一構件的迴轉角速度與自身扭矩反向時，可認為流經該構件的功率為從系統內向外流出功率。

圖 2 輸入、輸出特性

(2)節點分析法

以上基本的功率輸入、輸出方向判別原則，對於單行星排，可以該排行星輪與行星架迴轉副點(在此稱之為節點)為分析、判斷的依據點。如該排任意一個構件的扭矩方向與自身迴轉角速度方向相同，則該構件向節點輸入功率。反之，如該排任意一個構件的扭矩方向與自身迴轉角速度的方向相反，則該構件自節點處接受功率。以圖1所示雙行星輪為例，說明功率流的判斷分析方法。由扭矩和運動聯立方程得功率：

即：N_t1為正，向系統輸入功率，N_q1為負，從系統輸出功率，N_j1為正，向系統輸入功率。在對功率的流入或流出有了一個基本的判斷後，可取行星排α₁的行星輪迴轉軸心為節點，如圖3行星排1所示。N_t1為向節點輸入功率，N_q1為自節點處輸出功率，N_j1為向節點輸入功率。

圖 3 功率流向

同樣，對於第2行星排α₂，也可以用同樣的方法進行分析。取第2行星排的行星輪節點為分析對象，顯然，ω_t2=ω_q1，M_t2=-M_q1。則：N_t2=ω_q1×(-M_q1)，為正值，即為向節點輸入功率。而N_j2的功率流仍需結合角速度ω_j2及扭矩M_j2加以確定，仍由扭矩和運動聯立方程可

即：N_t2為正，向節點α₂輸入功率，N_j2為負，自節點處輸出功率，如圖3的α₂所示。

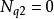
研究結論

(1)對行星輪系分析時，必須計算各構件的迴轉角速度、各構件扭矩，而節點分析法正是利用了各構件上的扭矩和角速度對該構件的功率流加以確定。因此，具有不增加分析計算工作量，且具有直觀明了、易於理解、不易出錯等特點。

(2)當套用三角形法對功率流進行分析時，必須進行構件速度三角形分析，以及構件的受力分析，然後再利用構件的扭矩、角速度、確定功率流向、分析計算過程過於複雜、不易理解。因此，利用節點分析法是分析計算功率流和循環功率的一種行之有效的方法。