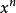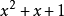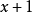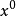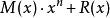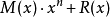簡介
循環冗餘校驗(英語:
Cyclic redundancy check,通稱“
CRC”)是一種根據網上數據包或
計算機檔案等數據產生簡短固定位數校驗碼的一種
散列函式,主要用來檢測或校驗數據傳輸或者保存後可能出現的錯誤。生成的數字在傳輸或者存儲之前計算出來並且附加到數據後面,然後接收方進行檢驗確定數據是否發生變化。一般來說,循環冗餘校驗的值都是32位的整數。由於本函式易於用二進制的
計算機硬體使用、容易進行數學分析並且尤其善於檢測傳輸通道干擾引起的錯誤,因此獲得廣泛套用。此方法是由W. Wesley Peterson於1961年發表。
CRC為
校驗和的一種,是兩個位元組數據流採用二進制除法(沒有進位,使用
XOR來代替減法)相除所得到的餘數。其中被除數是需要計算校驗和的信息數據流的二進制表示;除數是一個長度為
的預定義(短)的二進制數,通常用多項式的係數來表示。在做除法之前,要在信息數據之後先加上
個0.
CRC是基於
有限域GF(2)(即除以2的同餘)的
多項式環。簡單的來說,就是所有係數都為0或1(又叫做二進制)的多項式係數的集合,並且集合對於所有的代數操作都是封閉的。例如:
2會變成0,因為對係數的加法運算都會再取2的模數。乘法也是類似的:
我們同樣可以對多項式作除法並且得到商和餘數。例如,如果我們用x+x+x除以x+ 1。我們會得到:
這裡除法得到了商x+ 1和餘數-1,因為是奇數所以最後一位是1。
字元串中的每一位其實就對應了這樣類型的多項式的係數。為了得到CRC,我們首先將其乘以
,這裡n是一個固定多項式的
階數,然後再將其除以這個固定的多項式,餘數的係數就是CRC。
在上面的等式中,
表示了本來的信息位是111,
是所謂的
鑰匙,而餘數1(也就是
)就是CRC. key的最高次為1,所以我們將原來的信息乘上
來得到
,也可視為原來的信息位補1個零成為1110。
一般來說,其形式為:
這裡M(x)是原始的信息多項式。K(x)是
階的“鑰匙”多項式。
表示了將原始信息後面加上
個0。R(x)是餘數多項式,即是CRC“校驗和”。在通信中,傳送者在原始的信息數據M後附加上n位的R(替換本來附加的0)再傳送。接收者收到M和R後,檢查
是否能被
整除。如果是,那么接收者認為該信息是正確的。值得注意的是
就是傳送者所想要傳送的數據。這個串又叫做
codeword.
CRCs經常被叫做“
校驗和”,但是這樣的說法嚴格來說並不是準確的,因為技術上來說,校驗“和”是通過加法來計算的,而不是CRC這裡的除法。
“錯誤糾正編碼”(Error–Correcting Codes,簡稱ECC)常常和CRCs緊密相關,其語序糾正在傳輸過程中所產生的錯誤。這些編碼方式常常和數學原理緊密相關。例如常見於通信或信息傳遞上
BCH碼、
前向錯誤更正、Error detection and correction等。
CRC多項式規範
下面的表格略去了“初始值”、“反射值”以及“最終異或值”。
CRC標準化問題
由於CRC-12有三種常用的形式,所以CRC-12的定義會有歧義
在套用的CRC-8的兩種形式都有數學上的缺陷。
據稱CRC-16與CRC-32至少有10種形式,但沒有一種在數學上是最優的。
同樣大小的CCITT CRC與ITU CRC不同,這個機構在不同時期定義了不同的校驗和。
CRC與數據完整性
儘管在錯誤檢測中非常有用,CRC並不能可靠地校驗
數據完整性(即數據沒有發生任何變化),這是因為CRC多項式是線性結構,可以非常容易地
故意改變數據而維持CRC不變,參見CRC and how to Reverse it中的證明。我們可以用Message authentication code校驗數據完整性。
參見
總的分類
特殊技術參考
Adler-32
Fletcher's checksum