基本介紹
- 中文名：循環乘積碼
- 外文名：cyclic product code
- 提出時間：1965年
- 提出者：Burton H. O和Weldon E.J.
- 特點：編碼複雜度低
- 套用：空間通信系統
簡介,循環乘積碼的構造,循環乘積碼的糾錯特性,循環乘積碼的套用實例,
簡介
Burton H. O和Weldon E.J.在1965年用孫子定理構造了一種在兩個子碼碼長
和
互素情況下的循環乘積碼，並且導出了該碼的生成多項式以及糾隨機錯誤和糾突發錯誤能力。根據Burton H. O和Weldon E.J.的結果，1975年Lee和Cheng推斷出當 和 互素時，乘積碼的循環映射不止一種。
乘積碼是很早就提出的一種編碼方案，在Turbo碼提出以後發現乘積碼在採用Turbo解碼算法時具有很好的性能，因此又將其稱為Turbo乘積碼，並且得到廣泛地套用。循環乘積碼是乘積碼中一類特別的編碼方案，這類碼字是一類循環碼，因此具有編碼複雜低的特點；它同時也屬於乘積碼，因此對其採用Turbo解碼時具有很好的性能。
將循環乘積碼套用在空間通信系統的下行鏈路中，不僅能有效地提高星上的功率利用效率，而且能夠降低星上編碼器的複雜度，因此循環乘積碼是一類適合空間通信系統套用的糾錯碼。
循環乘積碼的構造
設
是一個
線性碼，
是一個
線性碼。則可以按照如圖1所示的方式構造一個
線性碼，即每個碼字是一個 列和 行的矩形陣列，其中每一行是一個 內碼字，每一列是一個 的碼字。這種二維的符合碼就稱之為 和 的乘積碼。從乘積碼的構造方法可以看出，其編碼過程是先對矩形陣列行編碼再列編碼。而如果這個乘積碼同時也是一個循環碼，則可以直接用移位暫存器實現其編碼，從而能夠有效地降低編碼器的硬體實現複雜度。
圖1 乘積碼的編碼結構
如果乘積碼的分量碼 和 都是循環碼，且它們的長度 和 是互質的，則按照適當的順序傳送碼字比特時，乘積碼
是一個循環碼，即為循環乘積碼。由於 和 互質，則存在一對整數a和b滿足：
一般的乘積碼輸出碼字時都是按行順序或列順序輸出，對於循環乘積碼用m(i，j)表示矩形陣列元素的輸出順序，則根據中國餘數定理對矩形陣列的傳送碼字排序即可得到循環乘積碼的傳送順序為：
令
和
分別表示碼字 和 的生成多項式，則循環乘積碼 的生成多項式為：
其中，GCD表示求最大公約數。求出循環乘積碼的生成多項式，則利用移位暫存器能夠很容易地實現其編碼過程，從而有效地降低了編碼器的硬體實現複雜度。
下面利用一個例子來說明循環乘積碼的構造和生成多項式的計算。令分量碼 為(15，10)漢明碼，則 =15，
=10，
。令分量碼 為(7，3)漢明碼， 則 =7，
=3，
。此時，循環乘積碼的碼長為
=105，信息位長度為
=30。且有1×15+(-2)×7=1，即15和7互質，a=l，b=-2。利用歐氏算法求出循環乘積碼的生成多項式為：
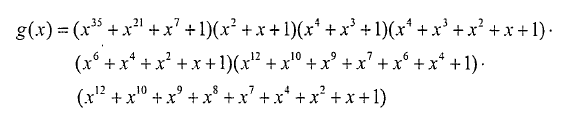
由上述第二個式子可得到該循環乘積碼的碼字傳送順序如圖2所示。
圖2 循環乘積碼的傳送順序
循環乘積碼的糾錯特性
假設兩個子碼分別能夠糾正
和
個突發錯誤。Burton H. O和Weldon E.J.導出的循環乘積碼在 和 互質時，其糾突發錯誤能力為：
只有當
時，
和當
時，
。
圖3列出了當兩個子碼均為BCH碼時，Burton H. O和Weldon E.J.導出的循環乘積碼的糾突發錯誤性能。
圖3
循環乘積碼的套用實例
這是一個循環乘積碼在空間通信系統中的套用實例。以(64，57)擴展漢明碼為子碼構造的乘積碼在採用Turbo解碼時具有很好的性能，並在實際通信系統中得到套用。為了使兩個子碼的碼長互質，利用(63，57)漢明碼和(64，57)擴展漢明碼為子碼構造循環乘積碼，則該碼字為碼率為0.8的(4032，3249)循環乘積碼。仿真條件為加性白高斯噪聲(AWGN)信道且採用BPSK調製。圖4給出了碼率為0．8時的香農限以及未編碼BPSK調製時的性能。圖4中還給出了以(63，57)漢明碼為子碼的乘積碼以及以(64，57)擴展漢明碼為字碼的乘積碼在採用Turbo解碼時的性能，可以預計的是以(63，57)漢明碼和(64，57)擴展漢明碼為子碼構造出的循環乘積碼在誤碼率(BER)為
時的性能介於前面兩種乘積碼之間，因此可以知道構造出的(4032，3249)循環乘積碼在BER為時距香農限約為1.6dB，而此時相對於未編碼系統有約6dB的編碼增益。又因為循環碼具有編碼複雜度低的特點，因此構造出的循環乘積碼具有編碼複雜皮低、解碼性能好的特點，適合於在空間通信系統中套用。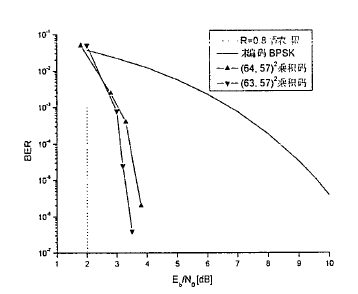
圖4 乘積碼的性能
