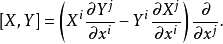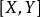復化李括弧

復化李括弧（complexification of Lie bracket）是實流形中李括弧經復化後的結果。

基本介紹

• 中文名：復化李括弧
• 外文名：complexification of Lie bracket
• 適用範圍：數理科學

簡介

復化李括弧是實流形中李括弧經復化後的結果。

李括弧復化給出C^∞(_CT(M))的李括弧，定義為

其中。

類似地，也可把李導數復化為_CT(M)的全張量代數上的導數。

李括弧

李括弧亦稱換位子，黎曼幾何中的一種運算。

李括弧即從兩個 C^r向量場得出一個新 C^r-1向量場的一種運算。

它可看成 𝒳^r(M)×𝒳^r(M) 到𝒳^r-1(M) 的映射：。使用局部坐標表示：

若

則

從而，是向量場。稱為向量場 X 和 Y 的李括弧，也稱為泊松括弧。

流形

流形是局部具有歐幾里得空間性質的空間，在數學中用於描述幾何形體。物理上，經典力學的相空間和構造廣義相對論的時空模型的四維偽黎曼流形都是流形的實例。

n維流形M的邊緣∂M是n-1維無邊緣流形。緊的無邊緣的連通流形稱為閉流形，非緊的無邊緣的連通流形稱為開流形。存在連通的但非仿緊的拓撲流形。一維的這種流形稱為長直線。