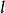徑向量子數

在不考慮自旋等內坐標時，求解一粒子在中心力場中的運動，由於力場的球形對稱性，採用球坐標（r，θ，φ）是方便的。此時，粒子的定態薛丁格方程可以通過分離變數法分成只同r有關的徑向部分和只同角度變數有關的角度部分。對於徑向部分的求解，可以發現徑向運動是量子化的。反映徑向運動量子化的量子數稱為徑向量子數。

基本介紹

• 中文名：徑向量子數
• 外文名：radial quantum number
• 定義：反映徑向運動量子化的量子數
• 套用學科：量子力學術語
• 範疇：理工科
• 涉及：薛丁格方程

概念

在不考慮自旋等內坐標時，求解一粒子在中心力場中的運動，由於力場的球形對稱性，採用球坐標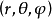 是方便的。此時，粒子的定態薛丁格方程可以通過分離變數法分成只同 有關的徑向部分和只同角度變數有關的角度部分。對於徑向部分的求解，可以發現徑向運動是量子化的。反映徑向運動量子化的量子數稱為徑向量子數。例如，求解氫原子和類氫離子中價電子的徑向薛丁格方程，發現徑向含糊 可用一個量子數 來標誌， 即為徑向量子數， 。 的取值與系統的能量有關：

因此在這個例子中， 也就是這個系統的主量子數，此時 。

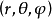
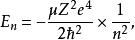
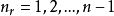
基本原理

在原子結構的研究中，電子在核場中運動時的勢函式往往是一個徑向函式，即

其中第一項為原子核靜電場，為核的原子序數。第二項是考慮原子內殼層電子對我們所研究的電子的禁止影響修正項。為內層電子云密度。

因為勢函式僅與有關，因而可將波函式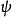分離變數為

將此表示代入定態薛丁格方程

則得到球坐標下的二個方程

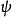
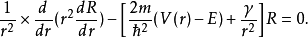
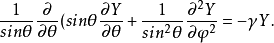
我們從量子力學教科書中可以知道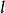：，為角動量量子數。