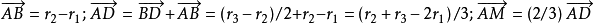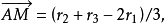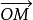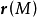徑向量(radius vector)亦稱向徑,又稱徑矢,一種特殊向量。以原點O為起點,以點M(x,y,z)為終點的向量稱做徑向量,記作r(M),或簡記作 r。由於徑向量的坐標與其終點M的坐標相同,所以它按基本向量的分解為:r=xi+yj+zk。
基本介紹
- 中文名:徑向量
- 外文名:radius vector
- 所屬領域:數學(空間解析幾何)
- 別名:向徑、徑矢
定義,線段的表示,例題解析,
定義
徑向量(radius vector)亦稱向徑,又稱徑矢。一種特殊向量,指始點在坐標原點O的向量,向徑 又稱為點P的位置向量,常以p表示點P的位置向量,這樣,點與位置向量有一一對應的關係。
又稱為點P的位置向量,常以p表示點P的位置向量,這樣,點與位置向量有一一對應的關係。

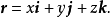
線段的表示
以點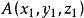 為起點而以點
為起點而以點 為終點的向量
為終點的向量 可以表示為:
可以表示為: 其中r2是B點的徑向量,而r1是A點的徑向量,因此向量
其中r2是B點的徑向量,而r1是A點的徑向量,因此向量 按基本向量的分解為
按基本向量的分解為
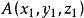







例題解析
【例1】三角形ABC的AB邊被點M、N分成三等份,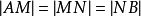 。設
。設 試求向量
試求向量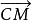 。
。
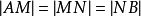

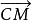
解:有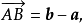 從而
從而 因為
因為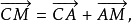 故
故
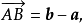

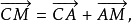

【例2】直線AM是三角形ABC中∠BAC的平分線,而M位於BC邊上,設 求
求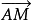 。
。

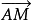
解:有 由三角形之內角平分線的性質,知有
由三角形之內角平分線的性質,知有 即
即 由此得
由此得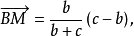 因為
因為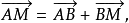 所以
所以 。
。



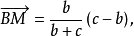
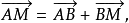

【例3】 和
和 為三角形ABC頂點的徑向量,求三角形之中線交點的徑向量。
為三角形ABC頂點的徑向量,求三角形之中線交點的徑向量。


解:有 (D是BC邊的中點);
(D是BC邊的中點);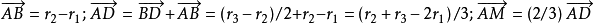 (M是中線的交點),所以
(M是中線的交點),所以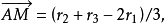 於是
於是