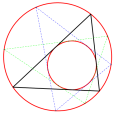
平面上給定兩條圓錐曲線,若存在一封閉多邊形外切其中一條圓錐曲線且內接另一條圓錐曲線,則此封閉多邊形內接的圓錐曲線上每一個點都是滿足這樣(切、內外接)性質的封閉多邊形的頂點,且所有滿足此性質的封閉多邊形的邊數相同。
最簡明的彭賽列閉合定理表示為:一個三角形外接於一個圓,內切一個圓,則外接圓可以有無數個內接三角形滿足其內切圓為上述的同一個。
彭賽列閉合定理展示了基於圓錐曲線關係上的一種“群結構”(group structure)關係——“彭賽列結構”(Poncelet type),表示為:有一個滿足一種結構的關係存在,則所有都滿足這種結構的關係都存在,可以擴展為更為高維的概念,彭賽列閉合定理只是這種結構關係的其中一種。
基本介紹
簡介,證明,
簡介
1746年,英國數學家Chapple發現了這樣一個性質:設兩圓圓心距d,大圓半徑R,小圓半徑r,在滿足公示d=R—2Rr(即後來被熟知的平面幾何歐拉定理公式)時,以R為外接圓半徑,以r 為內切圓半徑的三角形有無窮多個,這是第一個已知的“彭賽列結構”。
1813年,拿破崙對俄戰爭後,彭賽列被囚禁在俄羅斯的薩拉托夫,並在監獄中發現了這樣一個里程碑級的射影性質,他的第一個證明是一個某種意義上分析式證明。
1822年彭賽列在其出版的“Traitédes propriétés projectives des figures”中給出了另一個純粹的幾何、綜合性的證明。
1828年,雅可比(Jacobi)對橢圓函式利用“積分定理”(addition theorem)完成了該定理的另一種證明,從本質上來說,“積分定理”等價於彭賽列定理,其均揭示了橢圓曲線中存在的一種“群結構”性質。
證明
(部分)
當封閉多邊形邊數n=3時
△ABC內接一條圓錐曲線,內切一條圓錐曲線,△DEF外接於外錐線,其DE、DF與內錐線相切,則EF也與內錐線相切

n=3彭賽列閉合定理證明
當封閉多邊形邊數n=4時
四邊形ABCD外接一圓錐曲線,內切一圓錐曲線,則有四邊形A'B'C'D'同樣內接及外切這兩條圓錐曲線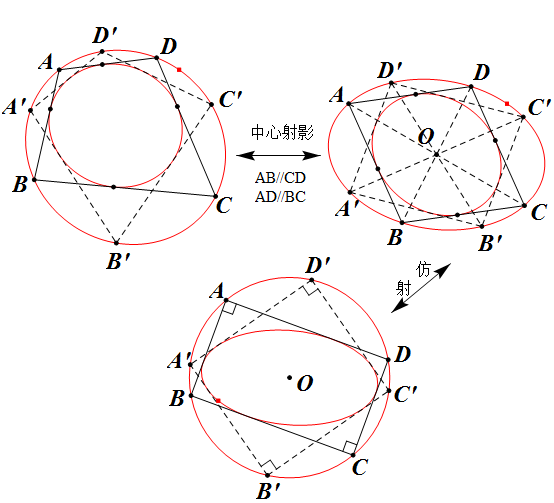

圖1 n=4彭賽列閉合定理證明
證明:在異於題設所在平面的空間上取一投影點,將右圖1(左上)中的AB、CD和AD、BC分別射影為一對平行線(右圖1右上),則四邊形ABCD為平行四邊形,且根據對稱性知此時兩條圓錐曲線被射影為中心重合的形式,其中心為平行四邊形中心O,再將其外圓錐曲線仿射為圓(右圖1下),因圓內接平行四邊形都為矩形,故利用蒙日圓性質知存在矩形A'B'C'D'滿足這樣的切接關係,逆射影回原題設,得證。