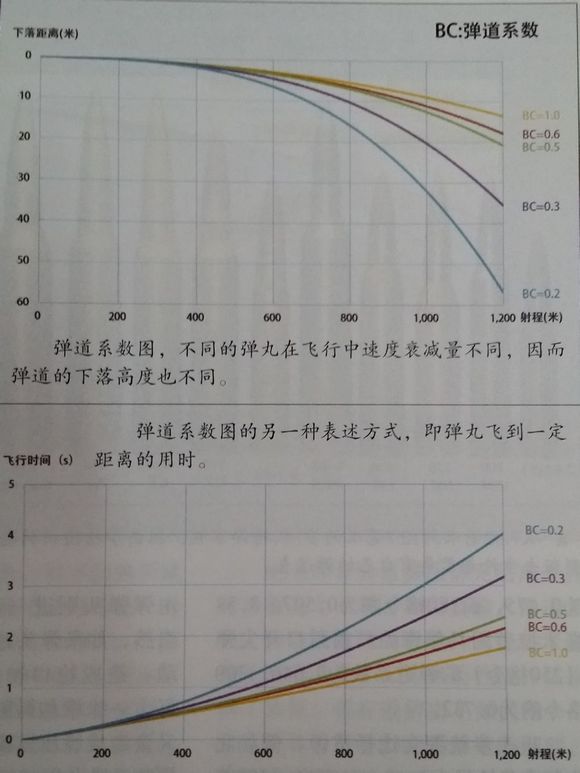
彈道係數(Ballistic Coefficient,簡稱BC)是一個用來衡量彈頭克服空氣阻力、維持飛行速度的能力的數學模式。決定彈道係數主要有兩個因素:截面密度和彈頭形狀。
基本介紹
- 中文名:彈道係數
- 外文名:Ballistic Coefficient
- 類型:數學模式
- 用途:衡量彈頭克服空氣阻力
- 學科:機械工程
- 簡稱:BC
介紹,模式,歷史,數據處理,彈道係數擬合,彈道外推,總結,
介紹
彈道外推算法是炮兵偵察校射雷達軟體系統的關鍵技術之一,雷達的外推精度很大程度上取決於外推算法的設計。當前的彈道外推算法主要包括兩大類,一是基於彈道模型的卡爾曼濾波估計算法,二是基於先驗樣本的機器學習算法。其中,卡爾曼濾波估計算法是炮兵偵察校射雷達裝備上採用的主要方法,該方法在建立濾波方程時受氣象條件和彈道等條件的影響較大,從而影響外推精度;基於樣本的算法由於受實際彈道樣本的限制,導致外推模型的實用性不高。
模式
先選擇一種“標準彈頭”(standard bullet),然後射擊數千次,詳細研究記錄其對空氣阻力(air drag)的反應以及整個彈道特性。根據這些特性進一步發展出“阻力數據表”(drag table),然後就可以對不同形狀和重量的彈頭在不同空氣狀況下的彈道做出近似的估計。“標準彈頭”的彈道係數是 1.0,如果有另一種彈頭的彈道係數是 0.5,表示它維持速度的能力只有“標準彈頭”的一半。決定彈道係數主要有兩個因素:截面密度(sectinoal density)和彈頭形狀(bullet shape)。一般來說截面密度越高,彈頭形狀越趨於尖形的,彈道係數越高。

歷史
彈道係數的發展要追溯到1881年,德國的克魯伯公司對一種鈍頭平底炮彈頭做了詳細的測試。俄國陸軍上校梅耶夫斯基(Mayevski)用克魯伯的數據發展出了一套數學模式來預測彈頭彈道,美國陸軍上校詹姆斯.英構司(James Ingalls) 然後就根據前二者的資料,印行了有關彈道的數據表。彈道係數的定義就是由英構司發明的。現代的彈道數據表已經修正了許多,也有新的數據表出現。但是最常用的 G1 模式,基本上還是根據當初的模式,而且在五百公尺距離內與市面上大部分的彈頭的特性還十分接近,因此還是一直沿用下來。
數據處理
彈道數據是進行彈道外推計算的基礎。由於雷達測量系統存在噪聲,在進行彈道外推計算時首先要進行彈道數據降噪處理。當前,彈道數據降噪方法主要包括Kalman濾波、多項式擬合方法等方法。前者在已知彈道參數條件下濾波精度較高,而彈道參數在實際外推時很難精確獲取,因此該方法使用受到很大限制; 後者不依賴於彈道參數,但精度不高。
小波變換是一種時間— 頻率分析方法,在時域和頻域內都能較好的表徵信號的局部持征,非常適合於探測正常數據中的瞬態反常現象,被譽為信號分析的“顯微鏡”,在自動控制、數據處理、信號分析等領域得到廣泛套用。
彈道測量數據序列中的真實數據和噪聲的時頻特性具有不同的特徵,真實數據表現為低頻特性或較為平穩的信號,噪聲信號在時域內處處存在且在頻域內表現為高頻信號。彈道測量數據的這種特性允許使用小波變換對數據進行濾波處理。
彈道係數擬合
彈道係數是表征彈丸本身及其與空氣之間相互作用特性的重要參數,不同的彈種具有不同的彈道係數,同一彈種在不同射角和射程時其彈道係數也略有不同,如何準確求出彈道係數對彈道計算至關重要。
該算法能將各種射擊條件的探測誤差都折合進彈道係數,因此如果僅從對彈道計算的影響來分析,則對於彈道的探測弧段來說彈道係數是最小二乘準則下最優的。
彈道擬合過程中需解決初始彈道係數的確定、彈道方程解算兩個關鍵問題。彈道擬合算法中彈道係數的初始值可以取零,但此時算法運耗時過多,從而影響算法的實時性。為此,要確定合理的初始彈道係數,以減少算法的運行時間。
六自由度剛體彈道方程和四自由度質心運動方程能夠較為精確的模擬彈丸飛行過程。考慮到六自由度剛體彈道方程非常複雜、計算量難以忍受、很多參數難以取得,常規彈藥較少使用。因此採用四自由度方程進行分析。
彈道外推
進行外推計算的基本原理是: 以探測彈道段上的某點為起始點向彈道起點( 或落點) 方向進行彈道積分,當積分至彈道高為給定值時停止,從而得到外推結果。
積分起點的諸元值可根據濾波後的測量數據計算得出,積分計算時的射擊條件取擬合彈道係數時的數值,當向起點積分時積分步長取負,向落點積分時積分步長取正。
總結
影響彈道外推的因素包括彈道數據處理、彈道方程解算、射擊條件的估計,其中彈道方程解算中彈道係數的估計尤為重要。用小波變換對彈道數據進行濾波處理,在最小二乘準則下計算擬合彈道係數,用彈道積分法進行外推計算,該方法能克服射擊條件探測誤差對外推帶來的影響,從而提高外推精度。仿真實驗表明,在雷達探測數據存在較大隨機噪聲的情況下,外推誤差在0~0.3%D的機率達到99.5%以上。