弱非退化條件是吳氏非退化條件的改進.由張景中、楊路等人提出.吳氏非退化條件要求升列中多項式初式不為0,即多項式關於主變元的最高次項係數不為0.弱非退化條件則只要求主變元各項係數不同時為0.
基本介紹
- 中文名:弱非退化條件
- 屬性:數學術語
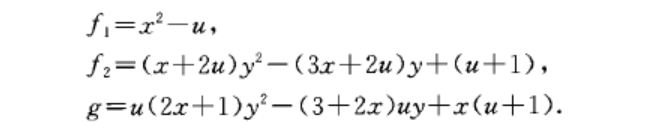

弱非退化條件是吳氏非退化條件的改進.由張景中、楊路等人提出.吳氏非退化條件要求升列中多項式初式不為0,即多項式關於主變元的最高次項係數不為0.弱非退化條件則只要求主變元各項係數不同時為0.
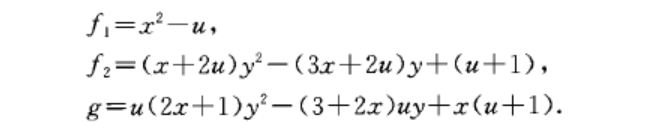
弱非退化條件是吳氏非退化條件的改進.由張景中、楊路等人提出.吳氏非退化條件要求升列中多項式初式不為0,即多項式關於主變元的最高次項係數不為0.弱非退化條件則只要求主變元各項係數不同時為0.弱非退化條件(weak nond...
弱非退化條件 吳氏非退化條件的改進。由張景中、楊路等人提出.吳氏非退化條件要求升列中多項式初式不為0,即多項式關於主變元的最高次項係數不為0。弱非退化條件則只要求主變元各項係數不同時為0。例如,設 f₁=x-u,f₂=(x+2u)y-(3x+2u)y+(u+1), g=u(2x+1)y-(3+2x)uy+x(u+1)。欲判斷...
近年來,受著名的DiPerna-Lions理論的啟發,係數滿足弱正則性條件的隨機微分方程(SDE)是國際上的熱點研究方向之一,在適當的Sobolev條件下人們證明了隨機可測映射流的存在唯一性,以及參考測度在流的作用下的擬不變性。 本項目取得了以下成果: (1)對於退化情形的Fokker-Planck方程,當它的擴散係數屬於Sobolev空間且...
7 基於弱非退化條件的代數簇的非混合分解 7.1 代數簇分解的基本概念 7.2 弱非退化條件簡介 7.3 代數簇的非混合分解算法 7.4 本章小結 8 總結與展望 8.1 主要工作總結 8.2 問題與展望 作者發表論文 參考文獻 附錄 作者簡介 季振義(1983年2月-),男,四川農業大學講師,長期從事計算機代數、多項式...
⑶用我們提出的弱非退化條件作零點分解,減少多餘分支。⑷子結式計算與數值檢驗配合,進行大範圍消元。⑸將所給方程組分解為三角列,便於機器證明和最終求解。經許多例子的演算,它比已知的各種方法有更好的效果。此法能在PC486機上解六變數循環方程,反解各種類型的六關節機器人問題,這是其它方法做不到的。非...
本課題主要利用KAM理論方法研究在較弱的非退化條件下,可逆系統和保面積映射等保守系統的滿足適當條件的不變環面經過小擾動能夠保持下來,並且頻率保持不變;研究在較弱非退化條件下,Gevrey光滑哈密頓在KAM環面附近的Birkhoff標準型,從而得到有效穩定性;研究圓周上的勻速旋轉在一個固定頻率的擬周期擾動下,共振不變環面...
