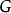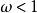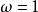鬆弛法

鬆弛法( relaxation method)是一種加速疊代方法，可視為高斯-賽德爾疊代法的推廣，對於數值計算各種問題所採用的疊代法，均可起到加速收斂的作用。此外還有超鬆弛法、群鬆弛法、逐次超鬆弛法等改進的鬆弛方法。

基本介紹

• 中文名：鬆弛法
• 外文名： relaxation method
• 相關概念：鬆弛因子
• 分類：超鬆弛法（SOR法）、低鬆弛法
• 領域：數值分析
• 學科：數學

簡介

鬆弛法是一種加速疊代方法，對於數值計算各種問題所採用的疊代法，均可起到加速收斂的作用。

此法產生於20世紀30年代，是基於變分思想的一種方法。其思想可描述如下： 假定把無重量的彈性弦拉成水平，然後在弦的一些點上加上負載，同時在每點上用與負載一樣大的力向上拉，此時弦依然處於平衡狀態，不產生彈性力，也沒有位移。有規則地逐漸減小各點向上的拉力，位移與彈性力也隨之產生，當各負載點向上的拉力減至零時，弦即處於鬆弛狀態，最終得到各負載點的位移。拉力減小的過程，就是逐步逼近鬆弛狀態的過程，鬆弛法由此得名。

一般地，我們可以使用鬆弛法解線性方程組。但鬆弛法的套用不限於此，對於微分方程及其他問題數值求解也是有用的。

此外還有超鬆弛法、群鬆弛法、逐次超鬆弛法等改進的鬆弛方法。

定義

設線性代數方程組為 。雅可比疊代和高斯-賽德爾疊代，在滿足收斂的充分條件時，儘管疊代過程是收斂的，但還存在收斂速度的問題。如果疊代法的收斂速度很慢，則會使計算的工作量過大。這時就必須尋求加速的方法。下面介紹的線性加速收斂的方法稱為鬆弛法。

以高斯-賽德爾疊代法為例。首先，由高斯-賽德爾疊代格式求得第 次疊代值 ，即

然後計算這個第 次疊代值與第 次疊代值之差，即 。最後在第 次疊代值的基礎上，直接加上這個差的一個倍數作為實際的第 次的疊代值，即

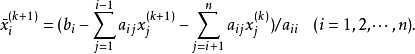
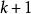
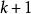
綜合以上過程，可以得到如下的疊代格式：

式中， 稱為鬆弛因子。

矩陣形式

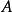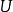設線性代數方程組為 。記 的對角線元素所成的對角矩陣為 ， ， 和 分別為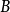 的下三角形和上三角形矩陣，則 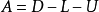，故疊代格式也寫為矩陣形式：

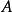
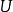
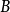
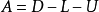
收斂性

疊代格式的矩陣形式可寫成

的形式，其中 稱為疊代矩陣。則上述疊代過程收斂的充分必要條件為

其中， 為 的譜半徑。

由此可得收斂的一個充分條件為

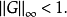
性質

1）當 時，稱為超鬆弛法，此時加大了 的比重；當 時，稱為亞鬆弛法或低鬆弛法；當 時，就是一般的高斯-賽德爾疊代法。

2）若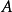 是對稱正定矩陣，且 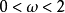，則SOR疊代法收斂。

3）若矩陣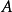嚴格對角占優，或不可約對角占優，且，則SOR疊代法收斂。

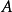
3）在實際套用中，可以根據係數矩陣的性質及其反覆計算的經驗來選定合適的鬆弛因子 ，以加快收斂速度。