廣義線性模型[generalize dlinear model]線性模型的擴展,通過聯結函式建立回響變數的數學期望值與線性組合的預測變數之間的關係。其特點是不強行改變數據的自然度量,數據可以具有非線性和非恆定方差結構。是線性模型在研究回響值的非常態分配以及非線性模型簡潔直接的線性轉化時的一種發展。
基本介紹
- 中文名:廣義線性模型
- 外文名:generalized linear model
- 適用範圍:數理科學
簡介
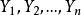
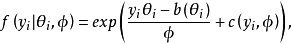
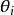



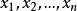
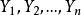
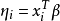
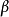
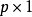
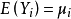
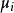
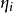
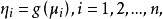
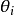
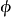
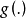
聯繫函式
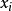
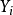
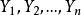
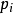
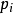
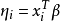
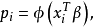
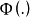
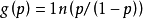
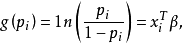
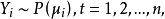
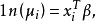
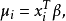

廣義線性模型[generalize dlinear model]線性模型的擴展,通過聯結函式建立回響變數的數學期望值與線性組合的預測變數之間的關係。其特點是不強行改變數據的自然度量,數據可以具有非線性和非恆定方差結構。是線性模型在研究回響值的非常態分配以及非線性模型簡潔直接的線性轉化時的一種發展。
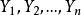
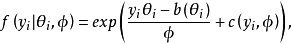
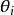



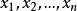
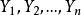
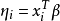
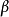
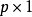
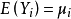
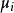
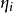
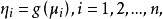
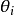
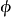
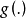
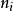
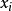
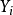
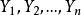
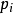
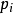
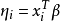
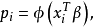
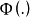
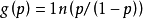
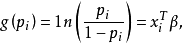
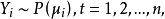
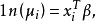
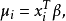
廣義線性模型[generalize dlinear model]線性模型的擴展,通過聯結函式建立回響變數的數學期望值與線性組合的預測變數之間的關係。其特點是不強行改變數據的自然度量,...
在機器學習中,線性模型(linear model)無法處理非線性套用,對模型稍加改變就可以處理非線性擬合。 對任意單調可逆函式g, 可以在求取逆函式後使用標準的線性擬合算法...
線性模型是一類統計模型的總稱,製作方法是用一定的流程將各個環節連線起來,包括線性回歸模型、方差分析模型,套用於生物、醫學、經濟、管理。...
《缺失數據下的廣義線性模型》是武漢大學出版社2013年出版的圖書,作者是肖枝洪、程新躍。...
內容介紹 《廣義線性模型導論》是格致方法定量研究系列之一種,《廣義線性模型導論》從廣義線性模型的理論提出入手,分析了經典回歸模型的發展及局限性,並列舉了藥物...
《廣義線性模型的擬似然法》是2011年中國科學技術大學出版社出版的圖書,作者是陳希孺。本書內容主要是關於廣義線性模型的幾種基本統計推斷形式(極大似然估計、假設...
線性模型簡單、直觀、便於理解,但是,在現實生活中,變數的作用通常不是線性的,線性假設很可能不能滿足實際需求,甚至直接違背實際情況。廣義加性模型是一種自由靈活的...
《線性和廣義線性混合模型及其統計診斷》是科學出版社2013年出版的圖書,作者是費宇、陳飛等。...
常用的統計模型有一般線性模型、廣義線性模型和混合模型。統計模型的意義在對大量隨機事件的規律性做推斷時仍然具有統計性,因而稱為統計推斷。常用的統計模型軟體有...
《現代數學:缺失數據下的廣義線性模型(專著版)》的內容除第1章為準備知識的介紹外,主要由三部分組成:第一部分包括第2章、第3章、第4章和第5章,主要討論缺失...
線性回歸模型套用及判別1 作者: 李元章 何春雄 責編: 詹志青 出版日期:2016年5月 裝幀: 簡裝 ISBN: 978-7-5623-4875-7 開本: 16 開 版次: 1-1 字數: ...
與多重線性回歸實際上有很多相同之處,最大的區別就在於他們的因變數不同,其他的基本都差不多,正是因為如此,這兩種回歸可以歸於同一個家族,即廣義線性模型(genera...
4.1 廣義線性模型(GLM) 4.2 勞吉斯特(Logistic)回歸模型 4.3 勞吉斯特模型擬合 4.4 勞吉斯特線性模型回歸係數的意義 4.5 利用SAS軟體擬合勞吉斯特模型 4.6 SAS...
