廣義二項分布

廣義二項分布(generalized binomial distribution)是一種離散型分布，屬於二項分布的一種推廣，亦稱“泊松二項分布”。設隨機變數ξ為n次泊松試驗中事件A發生的次數，稱ξ服從廣義二項分布，其分布形式為ξ=ξ₁+ξ₂++ξ_n，其中隨機變數ξ_i(i=1，2，…，n)是相互獨立的，且服從伯努利（兩點）分布。這時，ξ=k的機率P={ξ=k}等於有r個ξ_i取1，(n-r)ξ_i個取零時的機率之和。對於某些具體的廣義二項分布，其p_k遵循一定的規律，此時ξ的機率分布可用數學式來描述。

基本介紹

• 中文名：廣義二項分布
• 外文名：generalized binomial distribution
• 所屬學科：數學（統計學）
• 別名：泊松二項分布
• 屬性：離散型分布，是二項分布的推廣

基本介紹

服從二項分布的變數在第 次試驗中，其機率不變，即事件A出現(發生或成功)和不出現用 代表(不發生或不成功)的機率分別是p和q=1-p。如果上述機率在貝努里試驗中是隨試驗次序而變的，即有事件A出現(發生或成功)的機率為 而事件A不出現(用 代表)的機率為 。同樣若各次試驗結果相互獨立，這就構成了一種廣義的貝努里概型，即各次試驗中事件出現機率並非一定相等。

於是在 次試驗中事件A出現的次數這一隨機變數所服從的分布就構成了所謂廣義二項分布。設這一隨機變數為Z，它實際上是下列變數之和：

其中各項變數 相互獨立且都服從機率函式為

和

的0-1分布。可見Z並不像通常的二項分布那樣簡單，而是服從所謂廣義二項分布，如要求 機率，則需要對各種有r個取1， 個取0的情況按式(2)的0-1分布計算其相應的機率再按與式(1)相對應的機率值相加而得到。

相關結論

以下給出上述服從廣義二項分布的隨機變數Z的一、二階原點矩和二階中心矩如下：

不難看出，後文所述的二項分布的統計特徵量：均值和方差(見式(9)和(10))正是上式的特例。顯然，式(3)～(5)中，若，式(3)必然簡化為式(9)，而式(5)必然簡化為式(10)。

二項分布

伯努利(Bernoulli)概型

假定在一組固定條件下所進行的重複試驗(或觀測)是相互獨立的，即每一次試驗結果都不依賴於其他各次試驗結果，則這種試驗就稱之為重複獨立試驗。例如，在n次重複獨立試驗中，其結果的機率就可寫為

上式即稱之為“獨立試驗概型”，其最簡單形式就是著名的貝努里試驗概型。假定上述n次重複獨立試驗結果僅有兩種可能結果：A和，即事件出現(發生或成功)和不出現(不發生或不成功)，根據機率的性質，其相應的機率必為p和q=1-p。換言之，貝努里概型，可寫為

上式右端正是二項展開式的第m+1項，故伯努利概型又稱為二項分布(binomial distribution)。

分布函式

按照離散型分布函式的定義，必然有如下分布函式式：

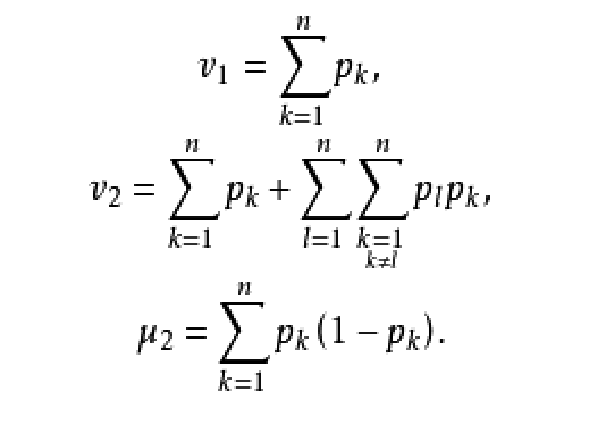
均值和方差

根據離散型變數均值的定義，不難推導出二項分布的總體均值和方差，以下僅給出一般公式：

由於二項式計算的對稱性，一般可通過制定特別的機率表格查算二項分布機率及其特徵參數，目前有不少統計軟體已將這類分布函式計算程式固化成套用非常方便的格式，人們只要從統計軟體包中直接調用即可。