度量方案(metric scheme)是一類結合方案,它由距離正則圖定義,若Γ為直徑d的距離正則圖,規定兩個頂點的距離為i時它們有第i種結合關係,則在Γ的頂點集合上有一個d個結合類的結合方案,稱為度量方案。
基本介紹
- 中文名:度量方案
- 外文名:metric scheme
- 所屬學科:數學(組合學)
- 簡介:由距離正則圖定義的一類結合方案
基本介紹
舉例
約翰生結合方案
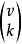
漢明結合方案
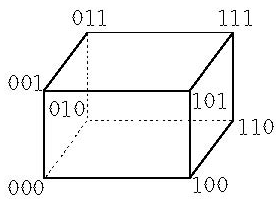 圖1
圖1
度量方案(metric scheme)是一類結合方案,它由距離正則圖定義,若Γ為直徑d的距離正則圖,規定兩個頂點的距離為i時它們有第i種結合關係,則在Γ的頂點集合上有一個d個結合類的結合方案,稱為度量方案。
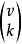
 圖1
圖1度量方案(metric scheme)是一類結合方案,它由距離正則圖定義,若Γ為直徑d的距離正則圖,規定兩個頂點的距離為i時它們有第i種結合關係,則在Γ的頂點集合上有一個...
軟體度量(software measurement)是對軟體開發項目、過程及其產品進行數據定義、收集以及分析的持續性定量化過程,目的在於對此加以理解、預測、評估、控制和改善。沒有...
《IT度量》是2003年清華大學出版社出版的圖書,作者是國際功能點用戶組織、方德英譯。...
軟體度量是對軟體開發項目、過程及其產品進行數據定義、收集以及分析的持續性定量化過程,目的在於對此加以理解、預測、評估、控制和改善。沒有軟體度量,就不能從軟體...
軟體過程方案是中科方德軟體有限公司研製的。...... 軟體過程方案度量分析工具 依據SEI推薦的度量指標以及高成熟度軟體企業的推薦度量,Qone平台內置了一批度量數據集,...
《精益軟體度量》是2013年人民郵電出版社出版的圖書,作者是張松,本書從精益理念的角度,嘗試重新梳理在中等規模到大規模軟體開發中度量體系設計和實施的思路。...
中國系統與軟體度量用戶組( China System and Software Measurement User Group),簡稱:軟體度量用戶組(SSM User Group),專注於系統與軟體度量領域的專業技術研究與...
本書通過具體的開發案例,詳細地介紹了如何套用一種有效的軟體測試方法——最重要測試(MIT)方法展開軟體測試,並提供了相應的測試度量及評估模板,用於指導測試工作。...
信息源可信度量,屬於信息檢索的範疇,是指在泛在網路的環境下,根據信息源的社會特徵、發布內容、來源設備等因素,對信息源的可信程度的綜合評估。信息源可信度量的...
《MDX解決方案》是2008年清華大學出版社出版的圖書,作者是(美)斯波福特。...... 《MDX解決方案》全面介紹了多維表達式(...17.3.3定義度量43417.3.4定義維度434...
廣州市度量行電子設備有限公司是一家專業致力於供排水過程監控、道路橋樑監測和供熱計量、無人機套用等領域內智慧型感測器的研發、生產、銷售的高新技術企業,以智慧型...
深圳市度量精密機械有限公司是多年從事機械設備,精密測量儀器生產、銷售、技術服務為一體的企業。...
在電子通信領域,波特率(Baud rate)即調製速率,指的是有效數據信號調製載波的速率,即單位時間內載波調製狀態變化的次數。它是對符號傳輸速率的一種度量,1波特即指...
《相關性度量技術及其在圖像處理中的套用》主要研究相關性定量度量技術及其在圖像處理中的套用,研究多變數間非線性相關程度的定量量化方法,提出非線性相關係數、相關...
