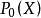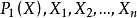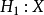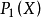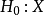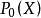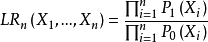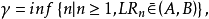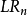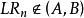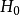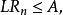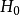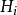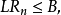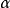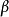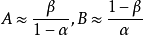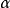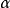序貫機率比檢驗

序貫機率比檢驗是數理統計學的一個分支，其名稱源出於亞伯拉罕·瓦爾德在1947年發表的一本同名著作，它研究的對象是所謂“序貫抽樣方案”，及如何用這種抽樣方案得到的樣本去作統計推斷。序貫抽樣方案是指在抽樣時，不事先規定總的抽樣個數（觀測或實驗次數）,而是先抽少量樣本,根據其結果，再決定停止抽樣或繼續抽樣、抽多少，這樣下去，直至決定停止抽樣為止。反之，事先確定抽樣個數的那種抽樣方案，稱為固定抽樣方案。

基本介紹

• 中文名：序貫機率比檢驗
• 外文名：Sequential probability ratio test,SPRT
• 出處：亞伯拉罕·瓦爾德
• 時間：1947年
• 提出者：亞伯拉罕·瓦爾德

定義

設隨機變數 X 的機率分布為 或 是樣本觀察值。而對備擇假設 服從分布 來檢驗零假設 服從分布 。

用似然比統計量

的序貫機率比檢驗方法是：確定兩個常數 A，B（0<A<1<B），設定停止法則為

即根據逐次實驗觀測數據計算 ，一旦 時就停止試驗，否則繼續試驗。試驗停止時，判決法則為

接受零假設 ，

拒絕零假設 ，接受備擇假設 ，

而常數 A，B 的確定與假設檢驗及犯第一類錯誤的機率 和犯第二類錯誤的機率 有關。近似地滿足下面關係：

以上的檢驗稱為序貫機率比檢驗（sequential probability ratio test）。

檢驗要點

此法在亞伯拉罕·瓦爾德的1947年的著作中有系統介紹，
其要點如下：設在原假設H₀和備擇假設H₁之下，隨機變數x的機率密度函式或機率函式隨機變數都已知,且分別為p₀(x)及p₁(x)，對x逐次觀測，第i次觀測的結果記為x_i，稱比值為樣本x₁，x₂，…，x_n的機率比。在固定抽樣方案之下，事先給定自然數n，對x進行n次觀測得x₁，x₂，…，x_n，計算。
定出一常數C（其值取決於檢驗水平α）,當λ_n≤C時，接受原假設H₀，否則拒絕。這樣在λ_n的值與C很接近時，H₀是否被接受的界限過於斷然，不大合理。瓦爾德將此修改為：指定兩個數A、B，A<B，根據各次觀測得的樣本x₁，x₂，…的值，依次計算機率比λ₁，λ₂，…。每次抽樣完畢，即算出λ_n，再與A、B比較，若λ_n≤A，則接受H₀；若λ_n≥B，則接收H₁，拒絕H₀；若A<λ_n<B，則繼續抽樣一次得x_n+1，計算出x_n+1再作上述比較，直到作出決定為止。這就是序貫機率比檢驗。至於A、B的定法,則取決於指定的兩種錯誤機率α和β（α,β都大於0，但很小）。
瓦爾德提供的近似公式是A=β/(1-α)，B=(1-β)/α。他也給出了這種檢驗法的平均抽樣次數和功效函式（見假設檢驗），並在1948年與美國統計學家J.沃爾弗維茨一起，證明了在一切兩種錯誤機率分別不超過α和β的檢驗類中，上述序貫機率比檢驗所需平均抽樣次數最少。

瓦爾德在其著作中也考慮了複合檢驗的問題，有許多統計學者研究了這種檢驗。瓦爾德的上述開創性工作，引起了許多統計學者對序貫方法的注意，並繼續進行工作，從而使序貫分析形成為數理統計學的一個分支。

序貫檢驗

[sequential test]

用序貫方法去檢驗一個假設的目的是：

①在同樣的可靠度下節省試驗次數；

②在不少問題中，為達到一定的可靠度，必須使用序貫方法。

序貫檢驗由停止法則和檢驗法則兩部分組成。停止法則說明何時停止抽樣，檢驗法則說明，在停止抽樣後，怎么根據已抽得多樣本去定是否接受元假設，其中平均抽樣次數（average sample number，ASN）和操作特徵函式(operating characteristic function，OCF)是刻畫一個序貫檢驗的兩個基本量。

所謂序貫檢驗就是按照某一個精度或可靠度給出一個停止規則，對於給定水平為 的一個檢驗，通過序貫抽樣給定一個檢驗，使用該檢驗在給定的精度下其功效大於顯著水平 。

舉例

一個產品抽樣檢驗方案規定按批抽樣品20件，若其中不合格品件數不超過 3，則接收該批，否則拒收。在此，抽樣個數20是預定的，是固定抽樣。若方案規定為：第一批抽出3個，若全為不合格品，拒收該批,若其中不合格品件數為x₁<3，則第二批再抽3-x₁個,若全為不合格品，則拒收該批，若其中不合格品數為x₂<3-x₁,則第三批再抽3-x₁-x₂個,這樣下去,直到抽滿20件或抽得3個不合格品為止。這是一個序貫抽樣方案，其效果與前述固定抽樣方案相同，但抽樣個數平均講要節省些。此例中，抽樣個數是隨機的，但有一個不能超過的上限20。有的序貫抽樣方案，其可能抽樣個數無上限，例如，序貫機率比檢驗的抽樣個數就沒有上限。
H.F.道奇和H.G.羅米格的二次抽樣方案是較早的一個序貫抽樣方案。1945年，C.施坦針對方差未知時估計和檢驗常態分配的均值μ（數學期望）的問題,提出了一個二次抽樣方案。依此方案,在事先給定了l>0和0<α<1後，可作出均值μ的一個置信區間，其置信係數為1-α，而長度不超過l。可以證明：當方差未知時，具有這種性質的置信區間在固定樣本的情況下不可能找到。由此可以看出序貫抽樣方案除了可節省抽樣量之外,還有一種作用，即為了達到預定的推斷可靠程度（這裡為置信係數）及精確程度（這裡是以區間長度來刻畫），有時必須使用序貫抽樣。

例如，估計一事件A的機率p(0<p<1)，給定ε>0及0<α<1，要找到這樣的估計，使能以不小於1-α的機率保證估計的相對誤差小於等於ε。可以證明，若用固定抽樣方案，事先指定自然數n，做n次試驗，每次觀察A是否發生，則不論n多么大，具有上述性質的不存在。但用下述序貫抽樣方案可得到這樣的：作試驗，觀察A是否發生，設到A第一次發生時已作了n₁次試驗，計算取其整數部分n_2，再作n₂次試驗，記n₂次試驗中A出現的次數為m，m/n₂，則有p(|-p|/p≤ε)≥1-α，而估計具有所指定的性質。