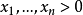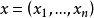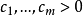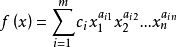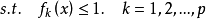幾何規劃是非線性規劃的一個分支。是最有效的最最佳化的方法之一。幾何規劃最初是由數學家R.J.達芬和 E.L.彼得森及C.M.查納等人於1961年在研究工程費用極小化問題基礎上提出的，直到1967年《幾何規劃》一書出版後才正式定名。幾何規劃的數學基礎是G.H.哈代的平均理論。由於幾何平均不等式的關鍵性作用，幾何規劃由此得名。幾何規劃的目標函式和約束條件均由廣義多項式構成 ，這是一類特殊的非線性規劃，利用其對偶原理，可以把高度非線性問題的求解轉化為具有線性約束的最佳化問題求解，使計算大為簡化。幾何規劃理論研究和算法軟體開發、發展都很快，並且在化工、機械、土木、電氣、核工程等部門的工程最佳化設計和企業管理、資源分配、環境保護以及技術經濟分析等方面都得到廣泛套用。
基本介紹
- 中文名：幾何規劃
- 外文名：geometric programming(GP)
- 性質：運籌學中的一個新興分支
- 正式定名：1967年
簡介,特徵,
簡介
非線性規劃的一個分支，20 世紀 60 年代中期由美國科學家達芬(R.J.Duffin)、彼得森(E.L.Peterson) 和齊納(C.Zener)首先提出，用以解決西屋公司(Westing House) 變壓器設計分析問題，後被廣泛套用於多類工程及管理之決策最佳化。
從工程設計費用最小化問題的研究中，發展了這類特殊非線性規劃的處理方法。這類特殊規劃的研究中，幾何平均不等式有著根本的作用，因而稱之為幾何規劃。它在化學和機械、土木、電氣、核工程以及管理科學等方面有許多套用。
特徵
幾何規劃的主要特徵在於其目標函式及約束函式的形式。
以正項幾何規劃為例，假設我們有 n 個正值實變數
並以向量
代表。
對於給定的 m 個正值實數
及
個一般實數
下列實函式
稱為正項多項式函式(posynomialfunction)。當
為 p+1個給定的正多項式函式，最基本的幾何規劃問題是尋求下列問題的最優解：
